8. [Algorithm] 플로이드 워셜 알고리즘 (최단 경로)
반응형
플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
지난 시간에 포스팅 했던 다익스트라 알고리즘의 경우, 한 지점에서 다른 특정 지점까지의 최단 경로를 구하는 알고리즘이다.
모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우에는 어떻게 해야할까?
바로 플로이드 워셜 알고리즘을 사용하면 된다.
- '모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우'에 사용할 수 있는 알고리즘
- 다익스트라의 경우 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 이후 해당 노드를 거쳐가는 경로를 확인하며 최단 거리 테이블을 갱신하는 방식으로 동작한다.
←→ 플로이드 워셜 알고리즘 또한 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. 하지만, 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다. - 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다. (모든 지점에서 다른 모든 지점까지의 최단 거리를 저장해야 하기 때문이다.)
←→ 다익스트라는 한 지점에서 다른 지점까지의 최단 거리이기 때문에 1차원 리스트에 저장한다. - 플로이드 워셜 알고리즘은 DP 알고리즘에 속한다. 왜냐하면 만약 노드의 개수가 N개 라고 할 떄, N번 만큼의 단계를 반복하며 점화식에 맞게 2차원 리스트를 갱신하기 때문에 DP라고 볼 수 있다.
플로이드 워셜 알고리즘의 점화식은 아래와 같다.
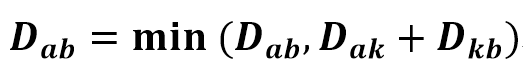
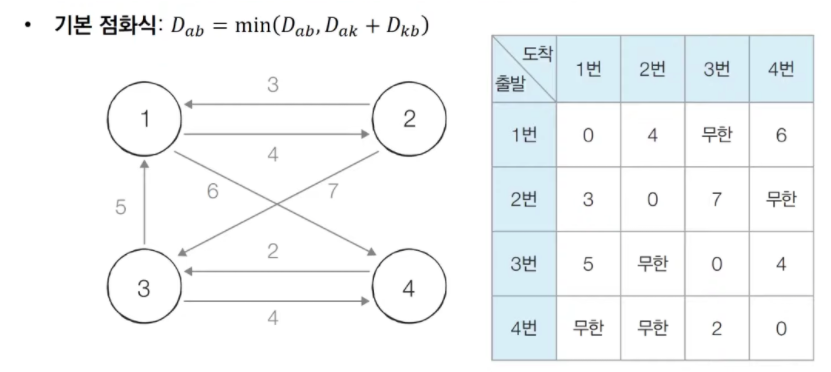
플로이드 워셜 알고리즘 그림으로 보기
- step 0 : 그래프의 노드와 간선에 따라 최단 거리 테이블을 갱신한다.
- step 1 : [step 1]에서는 단순히 1번 노드를 거쳐 가는 경우를 고려한다. 이때는 정확히 다음과 같이 6 = (_3)P(_2)가지 경우에 대해서만 고민하면 된다. 2차원 테이블에서는 다른 색으로 칠해 놓았는데, 계산해야 할 값들은 구체적으로 다음과 같다.
이 6가지 경우만 하나씩 확인하며 값을 계산하여 갱신한다. 예를 들어 D(_23) = min(D(_23), D(_21) + D(_13))은
'기존의 2번 노드에서 3번 노드로 가는 비용'보다 '2번 노드에서 1번 노드를 거쳐 3번 노드로 가는 비용이 더 작다면, 그것으로 갱신해주겠다는 의미를 가진다.
그래서 D(_23)의 값은 D(_23)과 D(_21) + D(_13) 중에 더 작은 값으로 교체된다.
다시말해 1을 거쳐 갈 때가 더 빠른 경우가 존재한다면 빠른 경우로 최단 거리를 갱신해주는 식이다.
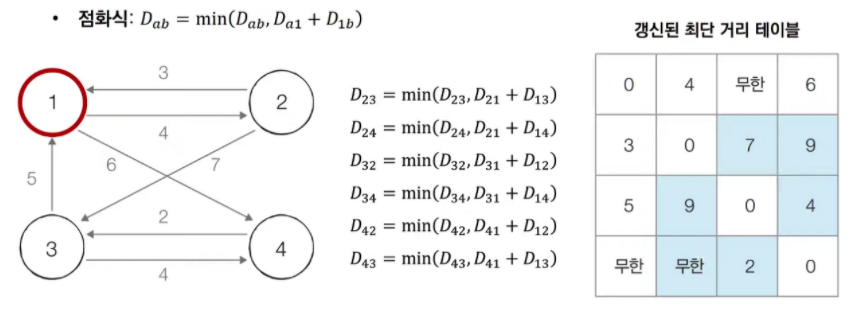
- step 2 : 마찬가지의 알고리즘을 [step 2]에 대해서도 수행할 수 있다.
이번에는 2번 노드를 거쳐 가는 경우를 계산해야 하므로 2번 노드를 제외한 1번, 3번, 4번 노드에서 2개의 노드를 뽑는 경우를 고려한다. 정확히 (1, 3), (1, 4), (3, 1), (3, 4), (4, 1), (4, 3) 으로 6가지 경우가 있다.
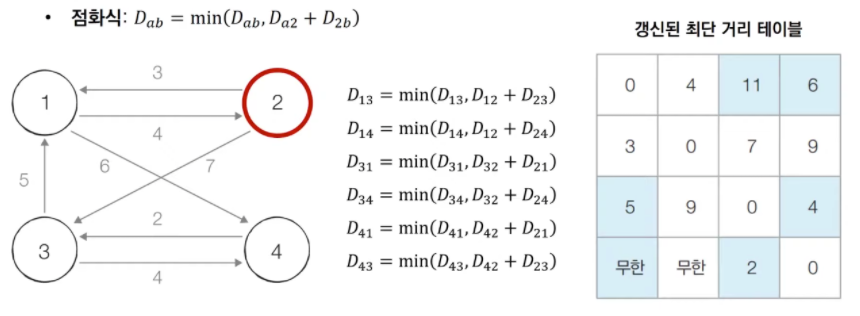
- step 3 : 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
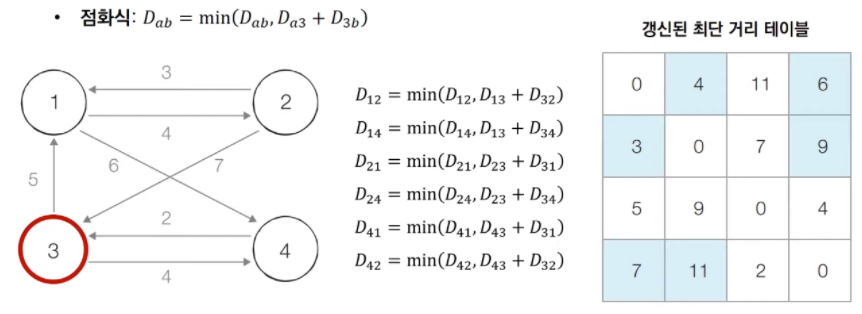
- step 4 : 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
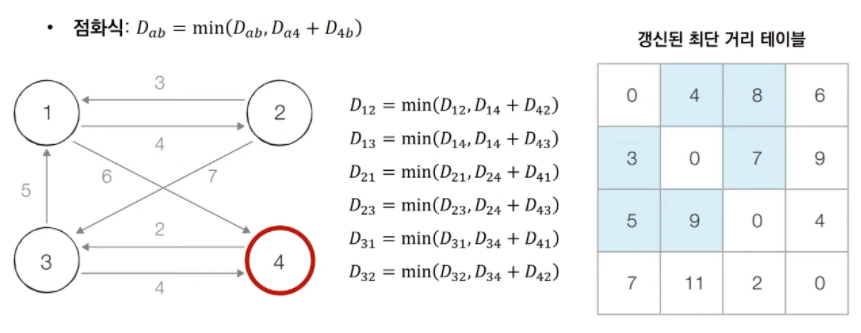
플로이드 워셜 알고리즘 코드 (Python)
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만ㄷ르고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력받아, 그 값으로 초기화
for _ in range(m):
# a에서 b로 가는 비용을 c라고 설정
a, b, c = map(int, input().split())
graph[a][b] = c
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 수행된 결과를 출력
for a in range(1, n + 1):
for b in range(1, n + 1):
if graph[a][b] == INF:
print('INFINITY', end=' ')
else:
print(graph[a][b], end=' ')
print()
'''
입력 예시
4
7
1 2 4
1 4 6
2 1 3
2 3 7
3 1 5
3 4 4
4 3 2
출력 예시
0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0
'''
플로이드 워셜 알고리즘 시간 복잡도
- 시간 복잡도는 O(N^3)
노드의 개수가 N개 일 때, N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 '현재 노드를 거쳐가는 모든 경로'를 고려한다. 따라서 시간 복잡도는 총 O(N^3)이다.
반응형
'Algorithm' 카테고리의 다른 글
| 10. [Algorithm] 크루스칼 알고리즘 (그래프 이론) (0) | 2023.03.27 |
|---|---|
| 9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set) (0) | 2023.03.24 |
| 7. [Algorithm] 다익스트라 알고리즘 (최단 경로) (0) | 2023.03.24 |
| 6. [Algorithm] 다이나믹 프로그래밍 (0) | 2023.03.21 |
| 5. [Algorithm] 이진 탐색 (0) | 2023.03.20 |
댓글
이 글 공유하기
다른 글
-
10. [Algorithm] 크루스칼 알고리즘 (그래프 이론)
10. [Algorithm] 크루스칼 알고리즘 (그래프 이론)
2023.03.27 -
9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set)
9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set)
2023.03.24 -
7. [Algorithm] 다익스트라 알고리즘 (최단 경로)
7. [Algorithm] 다익스트라 알고리즘 (최단 경로)
2023.03.24 -
6. [Algorithm] 다이나믹 프로그래밍
6. [Algorithm] 다이나믹 프로그래밍
2023.03.21