10. [Algorithm] 크루스칼 알고리즘 (그래프 이론)
크루스칼 알고리즘 (Kruskal Algorithm)

신장 트리 중에서 최소 비용으로 만들 수 있는 신장 트리를 찾는 알고리즘을 '최소 신장 트리 알고리즘' 이라고 하는데,
대표적인 최소 신장 트리 알고리즘으로는 크루스칼 알고리즘 이 있다.
크루스칼 알고리즘 을 사용하면 가장 적은 비용으로 모든 노드를 연결할 수 있다.
- 크루스칼 알고리즘은 대표적인 최소 신장 트리 알고리즘 이다.
- 그리디 알고리즘으로 분류된다.
그렇다면, 신장 트리란 무엇인가?
- 신장 트리 란 하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
→ 이때 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는 다는 조건은 트리 의 성립 조건이기도 함.
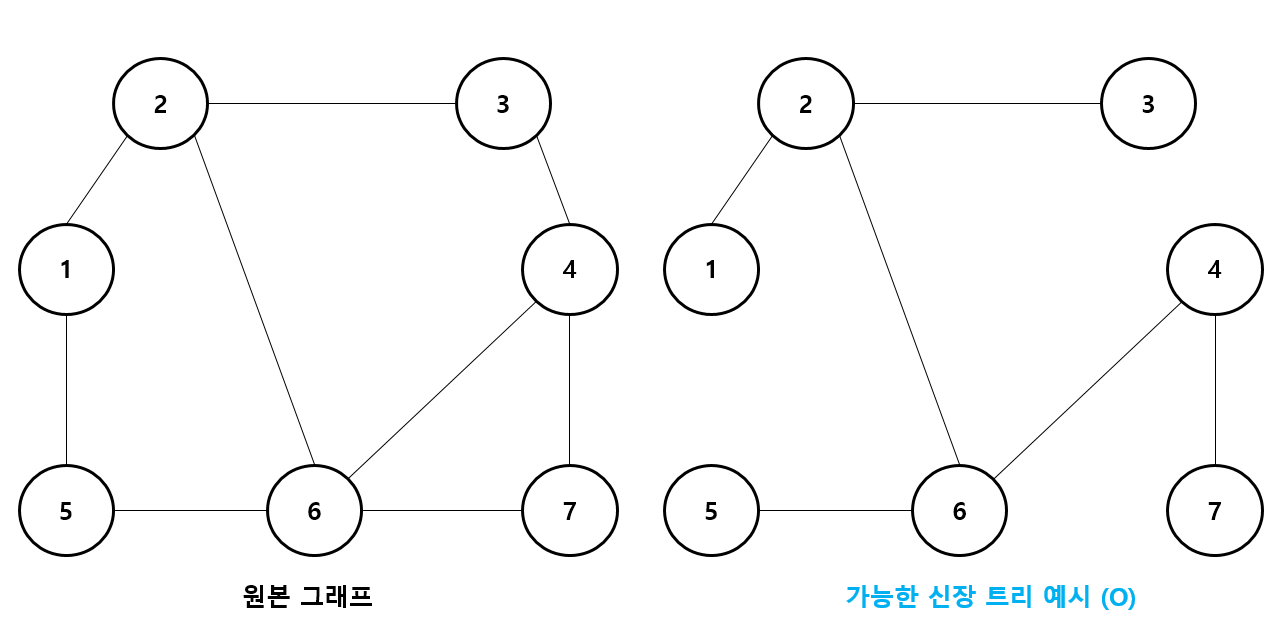
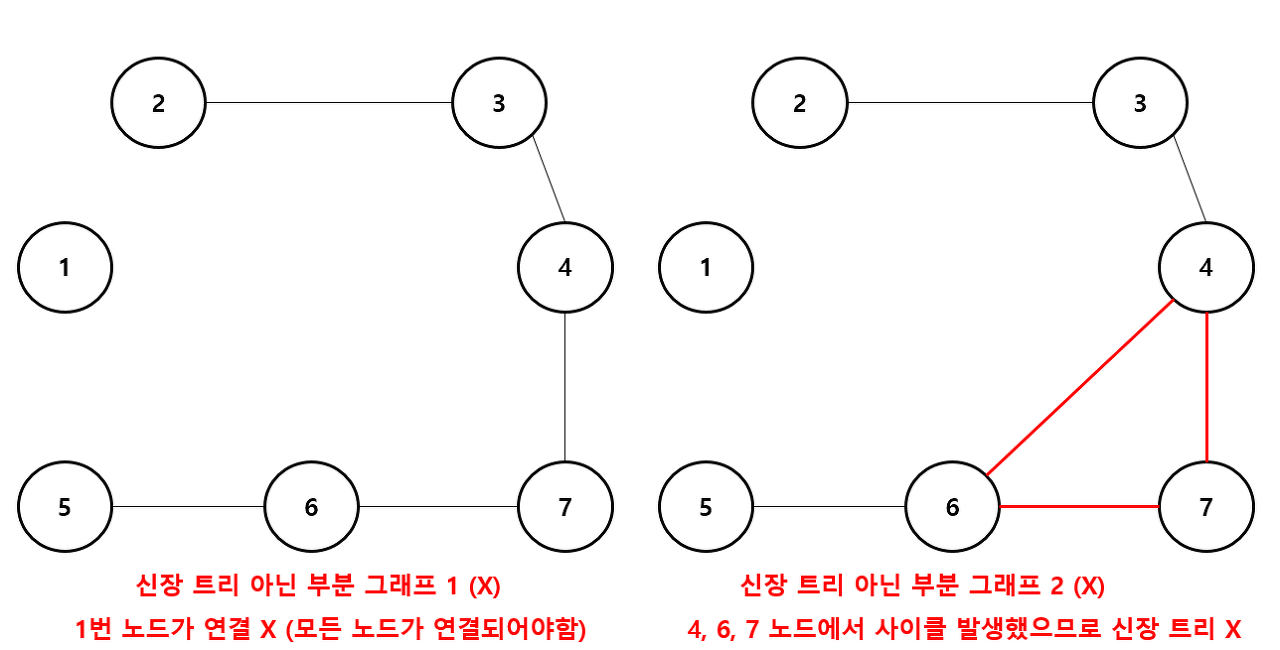
신장 트리는 알겠고.. 그러면 최소 신장 트리(Minimum Spanning Tree)는 무엇인가?
크루스칼 알고리즘 은 신장 트리 중에서도 최소한의 비용으로 만들 수 있는 최소 신장 트리를 찾는 알고리즘이다.
아래 그림을 통해 최소 신장 트리를 알아보자.
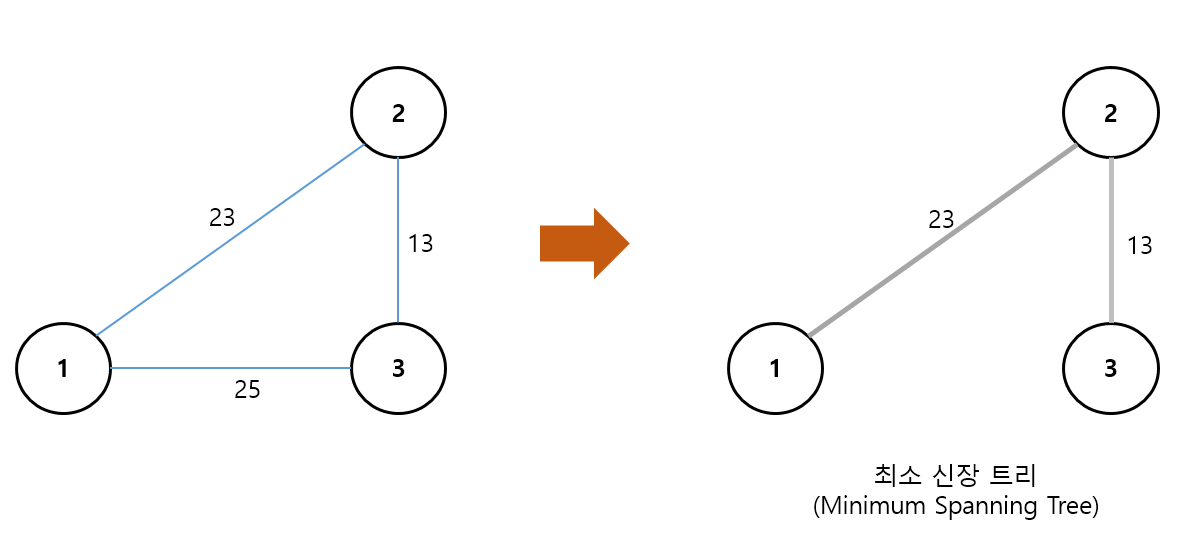
왼쪽 그래프에서 최소 신장 트리를 찾으면,
25를 제외한 2개의 간선(23+13)으로 이루어진 신장 트리가 바로 최소 신장 트리 가 된다.
즉, 신장 트리의 조건을 만족하면서 최소 비용으로 만들 수 있는 신장 트리가 최소 신장 트리 가 된다.
신장트리 라고도 하는 스패닝 트리는 다음과 같은 조건이 성립해야한다.
- N개의 정점을 가지는 그래프에서 최소 N-1 개의 간선으로 연결되어 있다.
- 그래프의 모든 정점을 포함한다.
그래프의 모든 정점을 가지고 있어야 신장트리의 조건이 만족되기 때문에, 간선의 갯수는 항상 N-1 개가 될 수 밖에 없고, N-1개의 간선과 N개의 정점으로 이루어진 그래프는 전체 그래프에 대한 사이클이 존재할 수 없기 때문에 항상 트리의 형태가 된다.
따라서 우리가 DFS나 BFS 로 탐색하면 각 정점들을 연결하게 되면 자연스럽게 Spanning Tree 가 완성이 된다.
크루스칼 알고리즘 동작 과정
크루스칼 알고리즘이 구체적인 동작 과정은 아래와 같다.
- 간선 데이터를 비용에 따라 오름차순으로 정렬한다.
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.
- 사이클이 발행하지 않는 경우 최소 신장 트리에 포함시킨다.
- 사이클이 발생하는 경우 최소 신장 트리에 포함시키지 않는다.
- 모든 간선에 대하여 2번의 과정을 반복한다.
크루스칼 알고리즘의 핵심 원리는 가장 거리가 짧은 간선부터 차례대로 집합에 추가하면 된다는 것이다.
다만, 사이클을 발생시키는 간선은 제외하고 연결한다. 이렇게 하면 항상 최적의 해를 보장할 수 있다.
아래 그림을 통해 이해해보자.
- step 0 : 그래프의 모든 간선 정보만 따로 빼내어 정렬을 수행한다.
(비용을 기준으로 오름차순 정렬을 한다. → 최소한의 비용으로 MST를 만들기 위함)
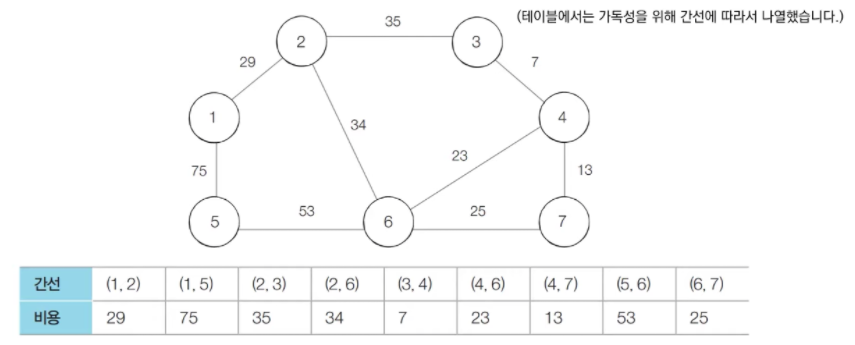
- step 1 : 비용이 가장 최소인 (3, 4)를 선택한 후 3번 노드와 4번 노드에 대하여 union 함수를 수행한다.
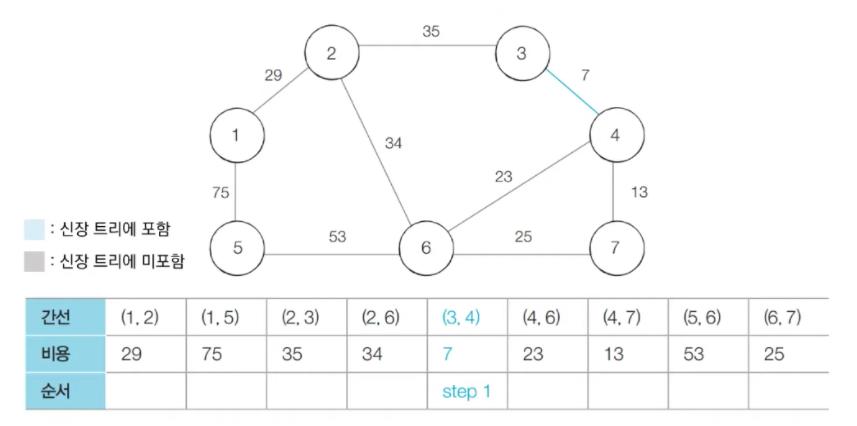
- step 2 : 방문하지 않은 간선들 중에서 가장 최소인 (4, 7)을 선택하여 처리한다.
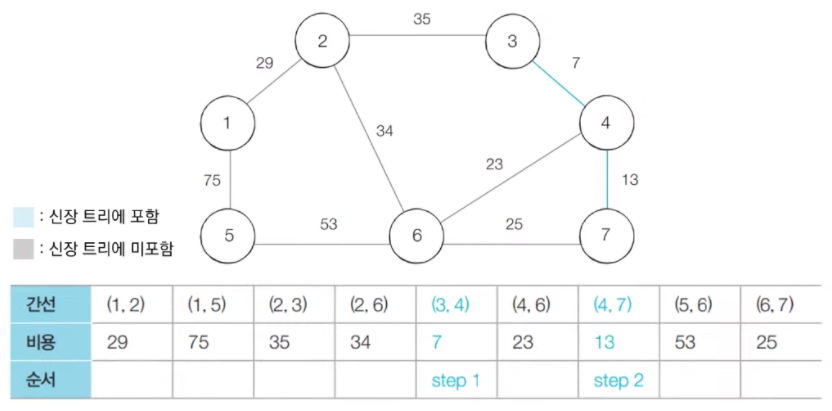
- step 3 : 방문하지 않은 간선들 중에서 가장 최소인 (4, 6)을 선택하여 처리한다.
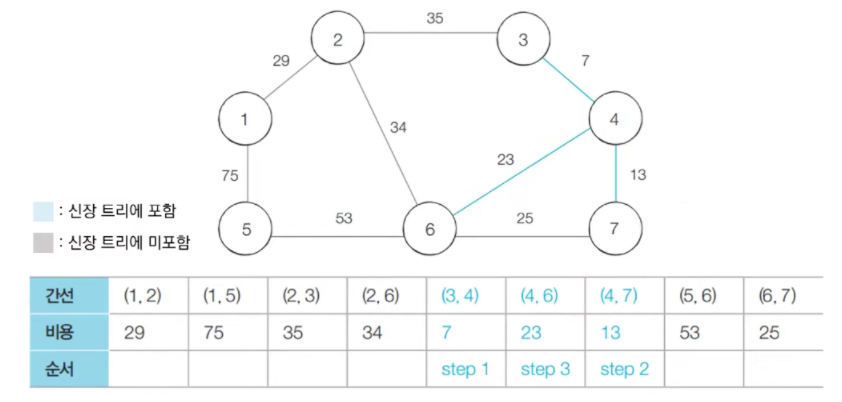
- step 4 : 방문하지 않은 간선들 중에서 가장 최소인 (6, 7)을 선택하여 처리한다.
하지만, (6, 7)을 방문할 경우(연결할 경우(=union()함수)) 사이클이 발생하므로(루트노드가 같으면) (6, 7) 간선을 연결하지 않는다.
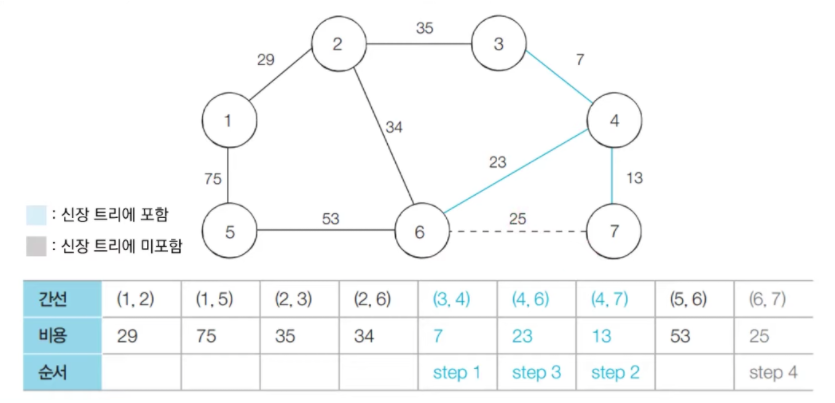
- step 5 : 방문하지 않은 간선들 중에서 가장 최소인 (1, 2)을 선택하여 처리한다.
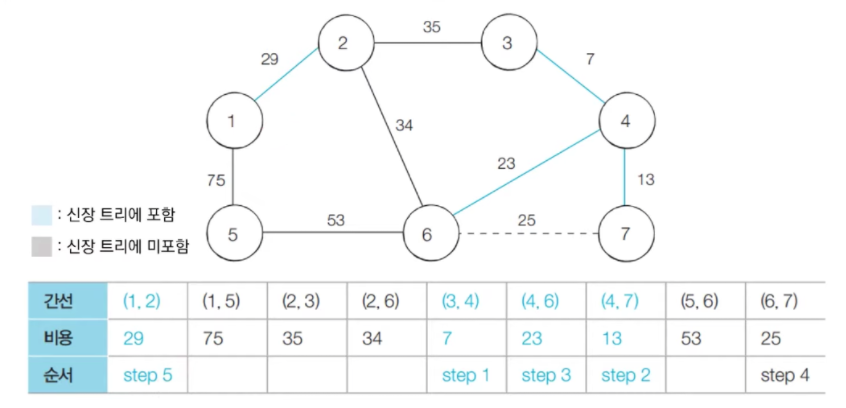
- step 6 : 방문하지 않은 간선들 중에서 가장 최소인 (2, 6)을 선택하여 처리한다.
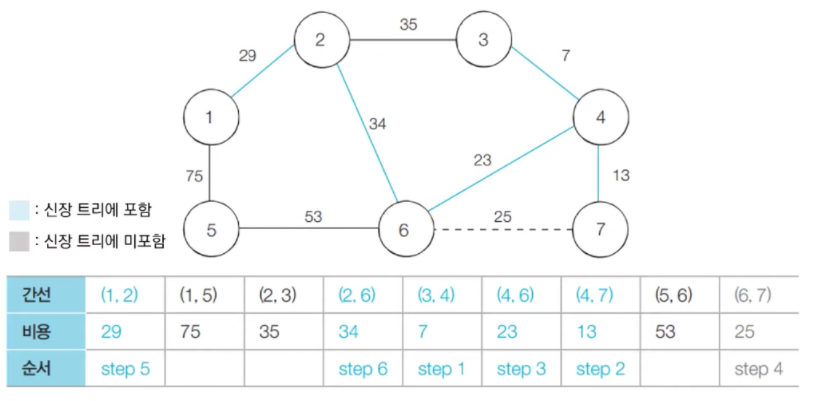
- step 7 : 방문하지 않은 간선들 중에서 가장 최소인 (2, 3)을 선택하여 처리한다. 하지만 (2, 3)을 연결할 경우에도 사이클이 발생하므로 연결하지 않는다.
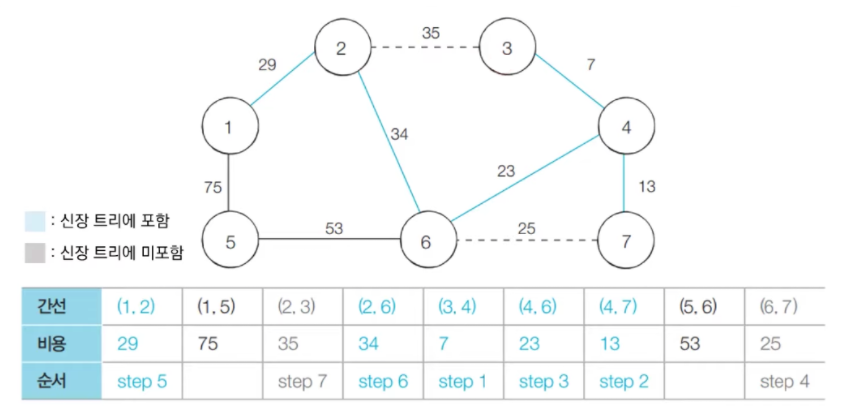
- step 8 : 방문하지 않은 간선들 중에서 가장 최소인 (5, 6)을 선택하여 처리한다.
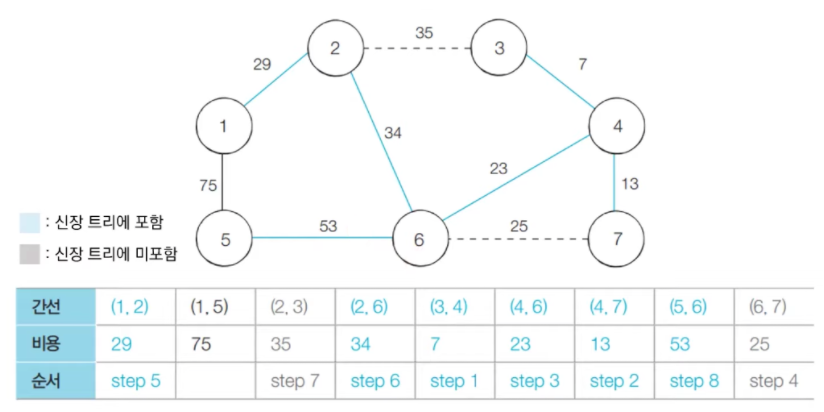
- step 9 : 방문하지 않은 간선들 중에서 가장 최소인 (1, 5)을 선택하여 처리한다. 마찬가지로 (1, 5)를 연결하면 사이클이 발생하므로 연결하지 않는다.
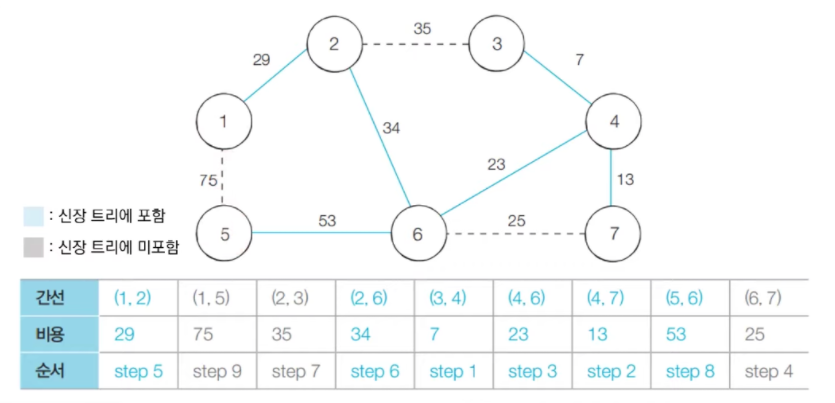
[최종 결과]
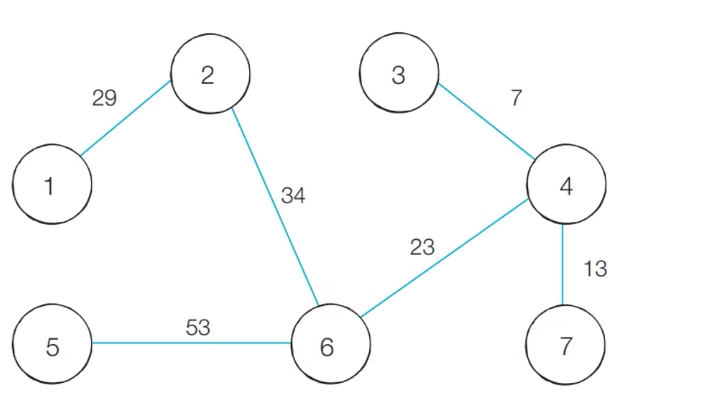
최소 신장 트리에 포함되어 있는 간선의 비용만 모두 더하면, 그 값이 최종 비용에 해당한다.
위 예시에서는 총 비용이 159이다.
크루스칼 알고리즘 코드 (Python)
크루스칼 알고리즘을 코드로 구현할 때, 앞서 공부한 union-find 알고리즘을 이용하여 구현한다.
# 특정 원소가 속한 집합을 찾기
import sys
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent,parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, x, y, rank):
rootX = find_parent(parent, x)
rootY = find_parent(parent, y)
# rank가 큰 트리에 작은 트리를 붙인다.
if rank[rootX] < rank[rootY]:
parent[rootX] = rootY
elif rank[rootX] > rank[rootY]:
parent[rootY] = rootX
else: # 만약 rank가 같다면 임의로 rootX 트리에 rootY 트리를 붙인다.
parent[rootY] = rootX
rank[rootX] = rank[rootX]
# 크루스칼
def kruskal():
total_weight = 0
# [1] 간선들을 가중치가 적은 순서대로 오름차순 정렬한다.
edges.sort()
# [2] 간선들을 하나씩 추출하여 연결한다.
for weight, v1, v2 in edges:
if find_parent(parent, v1) != find_parent(parent, v2): # 같은 집합(트리)에 있는 경우 union하지 않는다. 사이클이 생기기 떄문이다.
union_parent(parent, v1, v2, rank)
total_weight = total_weight + weight
return total_weight
# 노드의 개수와 간선 (union 연산)의 개수 입력받기
v, e = map(int, input().split())
parent = [i for i in range(v + 1)]
rank = [0 for i in range(v + 1)]
edges = []
for i in range(e):
v1, v2, w = map(int, sys.stdin.readline().rstrip().split())
edges.append([w, v1, v2])
answer = kruskal()
print(answer)
'''
입력 예시
7 9
1 2 29
1 6 75
2 3 35
2 6 34
3 4 7
4 6 23
4 7 13
5 6 53
6 7 25
출력 예시
159
'''
시간 복잡도
- 시간 복잡도는 O(ElogE)
크루스칼 알고리즘은 간선의 개수가 E 개일 때, O(ElogE) 의 시간 복잡도를 가진다. 왜냐하면 시간이 가장 오래 걸리는 부분이 간선을 정렬하는 작업이며, E 개의 데이터를 정렬했을 때의 시간 복잡도는 O(ElogE) 이기 때문이다. → (Python 에서 .sort() 함수는 퀵 정렬을 기본으로 하며 퀵 정렬의 시간 복잡도는 O(NlogN) 이다.)
크루스칼 내부에서 사용되는 서로소 집합 알고리즘의 시간 복잡도는 정렬 알고리즘의 시간 복잡도보다 작으므로 무시한다.
'Algorithm' 카테고리의 다른 글
| 11. [Algorithm] 위상 정렬 (그래프 이론) (0) | 2023.03.27 |
|---|---|
| 9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set) (0) | 2023.03.24 |
| 8. [Algorithm] 플로이드 워셜 알고리즘 (최단 경로) (0) | 2023.03.24 |
| 7. [Algorithm] 다익스트라 알고리즘 (최단 경로) (0) | 2023.03.24 |
| 6. [Algorithm] 다이나믹 프로그래밍 (0) | 2023.03.21 |
댓글
이 글 공유하기
다른 글
-
11. [Algorithm] 위상 정렬 (그래프 이론)
11. [Algorithm] 위상 정렬 (그래프 이론)
2023.03.27 -
9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set)
9. [Algorithm] Union-Find 알고리즘 (서로소 집합 Disjoint-Set)
2023.03.24 -
8. [Algorithm] 플로이드 워셜 알고리즘 (최단 경로)
8. [Algorithm] 플로이드 워셜 알고리즘 (최단 경로)
2023.03.24 -
7. [Algorithm] 다익스트라 알고리즘 (최단 경로)
7. [Algorithm] 다익스트라 알고리즘 (최단 경로)
2023.03.24