[백준] 14567번 선수과목 (feat. 위상 정렬)
https://www.acmicpc.net/problem/14567

문제 분석
- 첫 번째 단계(문제 요약 및 조건 파악)
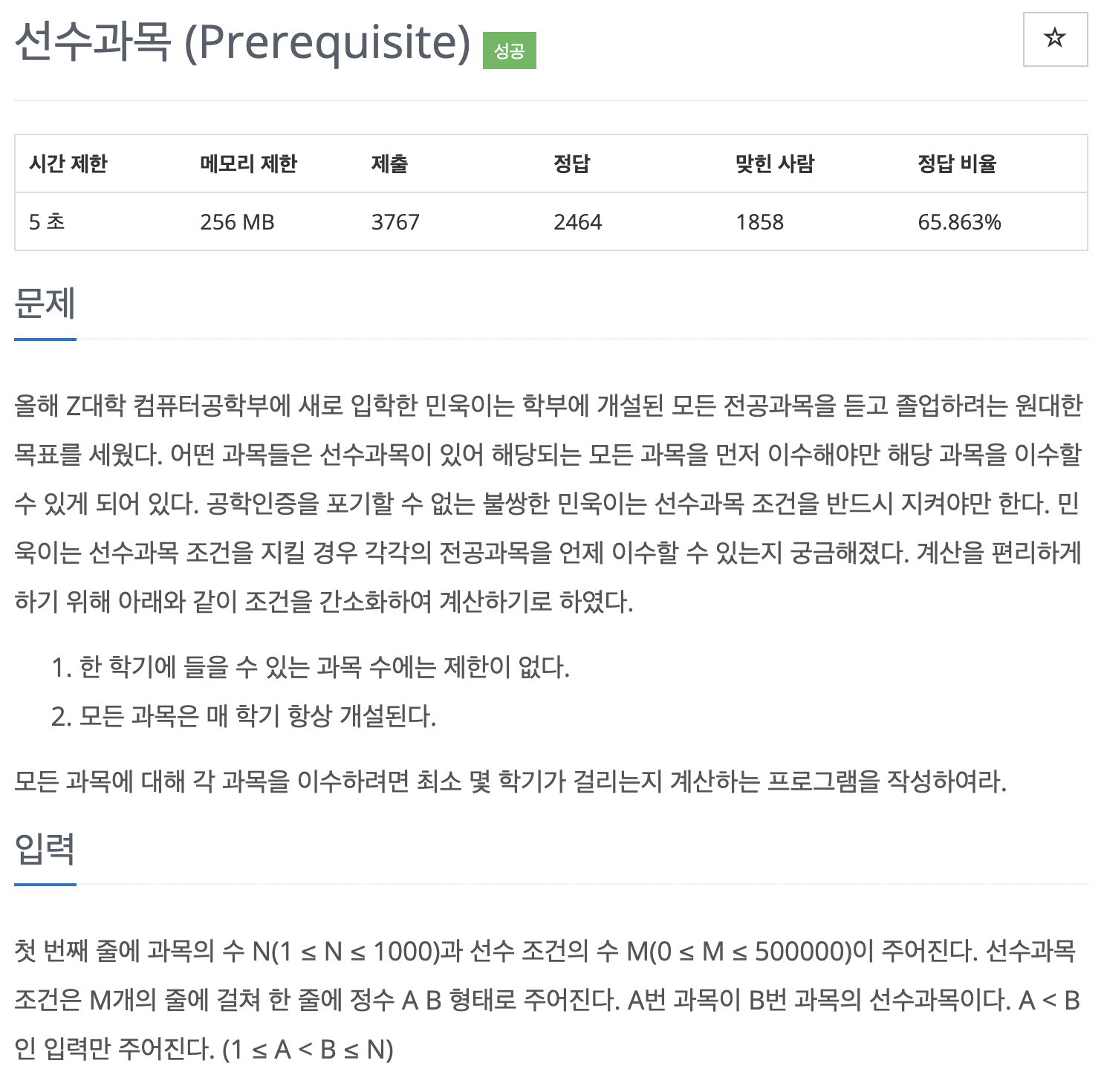
어떤 과목들은 선수과목이 있음.
선수과목 조건을 반드시 지키려고함.
1. 한 학기에 들을 수 있는 과목 수에는 제한이 없음.
2. 모든 과목은 매 학기 항상 개설.
모든 과목에 대해 각 과목을 이수하려면 최소 몇 학기가 걸리는지 계산하는 프로그램을 작성하여라.
- 입력
첫 번째 줄에 과목의 수 N(1 <= N <= 1000), 선수 조건의 수 M(0 <= M <= 500000)
M개의 줄에 걸쳐 A B 가 주어지는데, A번 과목이 B번 과목의 선수과목이라는 의미다. A < B 인 입력만 주어짐.(1 <= A < B <= N)
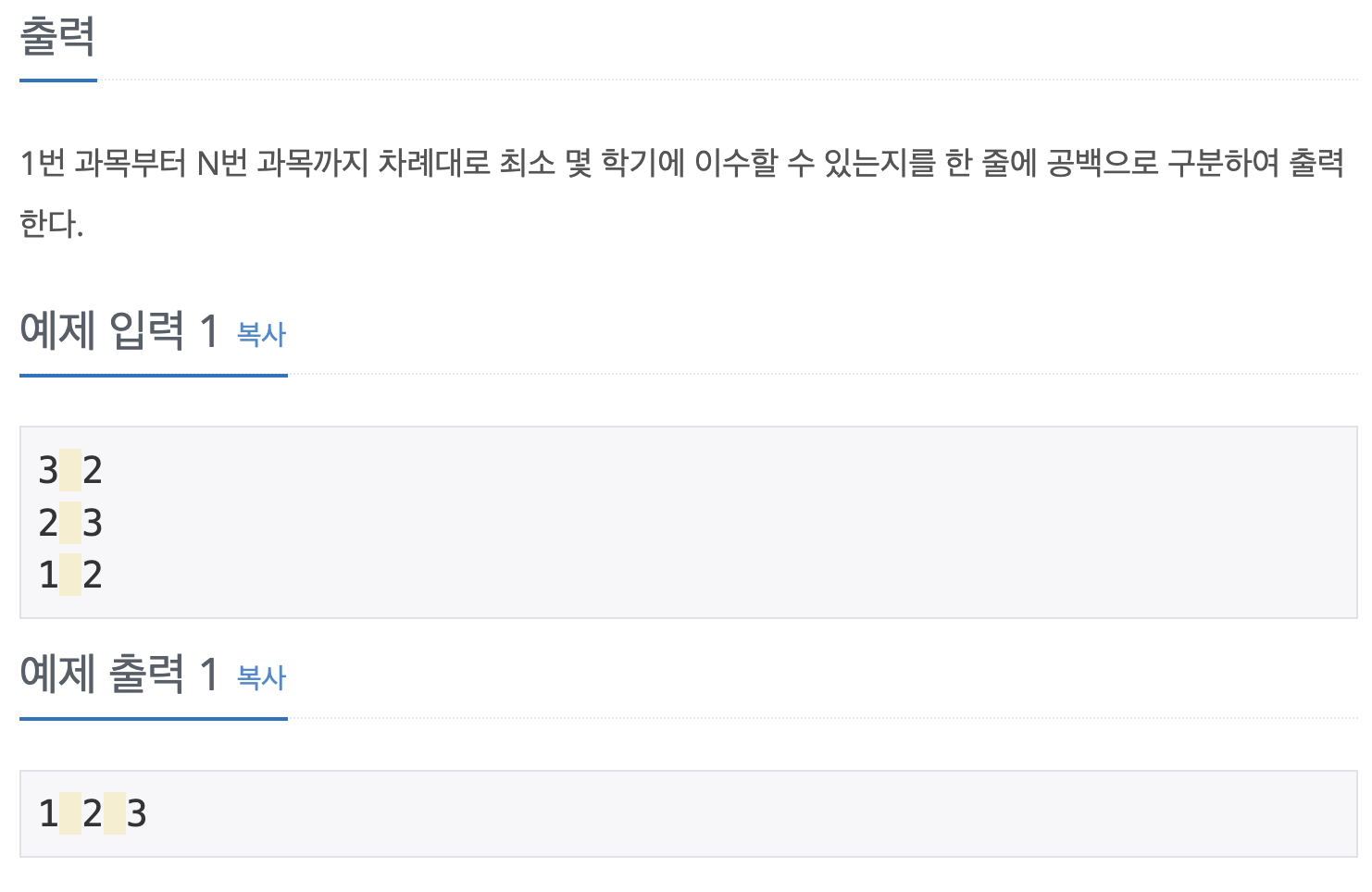
- 출력
1번 과목부터 N번 과목까지 차례대로 최소 몇 학기에 이수할 수 있는지를 한 줄에 공백으로 구분하여 출력한다.
- 두 번째 단계(문제 핵심 파악)
생각해보면, 예를 들어 선수과목 조건으로 a b 가 주어지면,
a는 b의 선수과목이라는 뜻이고, 만약 a를 1학기에 이수하면, b는 2학기부터 이수할 수 있다.
즉, 진입차수를 파악하는 것이 핵심이다.
한 학기에 들을 수 있는 과목 수에는 제한이 없으므로, 위상정렬을 수행하면서 처음에 진입차수가 0인 것들은 or 입력에 없는 과목은 무조건 1학기에 이수가 가능 할 것이다.
ii)
일반적인 위상정렬을 수행한 결과는 1 4 6 2 3 5 가 나왔는데,
문제의 출력 조건에 따라 내가 원하는 것은 각 과목별 이수 가능 학기인 1 2 2 1 3 1 이다.
1은 1학기
4은 1학기
6은 1학기
2는 2학기
3은 2학기
5는 3학기 이다.
이때 1, 4, 6은 처음에 진입차수가 0이므로 처음에 큐에 들어갈 것이다. 처음에 큐에 들어가는 것들은 모두 1학기로 저장하도록 해야한다.
그다음에 now 노드와 연결된 노드의 진입차수가 0이 될 때 해당 연결된 노드를 큐에 넣게 되는데,
이때 연결된 노드의 이수 가능 학기는 now 노드의 이수가능학기 + 1 일 것이다.
enrollment_semester라는 리스트를 선언해서 이수가능 학기를 저장해주자.
코드 작성
'''
어떤 과목들은 선수과목이 있음.
선수과목 조건을 반드시 지키려고함.
1. 한 학기에 들을 수 있는 과목 수에는 제한이 없음.
2. 모든 과목은 매 학기 항상 개설.
모든 과목에 대해 각 과목을 이수하려면 최소 몇 학기가 걸리는지 계산하는 프로그램을 작성하여라.
- 입력
첫 번째 줄에 과목의 수 N(1 <= N <= 1000), 선수 조건의 수 M(0 <= M <= 500000)
M개의 줄에 걸쳐 A B 가 주어지는데, A번 과목이 B번 과목의 선수과목이라는 의미다. A < B 인 입력만 주어짐.(1 <= A < B <= N)
- 출력
1번 과목부터 N번 과목까지 차례대로 최소 몇 학기에 이수할 수 있는지를 한 줄에 공백으로 구분하여 출력한다.
i)
생각해보면, 예를 들어 선수과목 조건으로 a b 가 주어지면,
a는 b의 선수과목이라는 뜻이고, 만약 a를 1학기에 이수하면, b는 2학기부터 이수할 수 있다.
즉, 진입차수를 파악하는 것이 핵심이다.
한 학기에 들을 수 있는 과목 수에는 제한이 없으므로, 위상정렬을 수행하면서 처음에 진입차수가 0인 것들은 or 입력에 없는 과목은 무조건 1학기에 이수가 가능 할 것이다.
ii)
일반적인 위상정렬을 수행한 결과는 1 4 6 2 3 5 가 나왔는데,
문제의 출력 조건에 따라 내가 원하는 것은 각 과목별 이수 가능 학기인 1 2 2 1 3 1 이다.
1은 1학기
4은 1학기
6은 1학기
2는 2학기
3은 2학기
5는 3학기 이다.
이때 1, 4, 6은 처음에 진입차수가 0이므로 처음에 큐에 들어갈 것이다. 처음에 큐에 들어가는 것들은 모두 1학기로 저장하도록 해야한다.
그다음에 now 노드와 연결된 노드의 진입차수가 0이 될 때 해당 연결된 노드를 큐에 넣게 되는데,
이때 연결된 노드의 이수 가능 학기는 now 노드의 이수가능학기 + 1 일 것이다.
enrollment_semester라는 리스트를 선언해서 이수가능 학기를 저장해주자.
'''
# 과목의 수 n, 선수 조건의 수 m
import sys
from collections import deque
n, m = map(int, input().split())
# 과목간의 관계를 저장 할 그래프
graph = [[] for i in range(n + 1)]
# 진입 차수를 저장할 리스트
indegree = [0 for i in range(n + 1)]
# 이수 가능 학기를 저장할 리스트
enrollment_semester = [0 for i in range(n + 1)]
# 과목간의 관계 입력 받기
for i in range(m):
a, b = map(int, sys.stdin.readline().rstrip().split())
graph[a].append(b)
indegree[b] = indegree[b] + 1
# 위상 정렬 함수
def topoloy_sort():
result = [] # 결과를 저장할 리스트
q = deque() # 큐 선언
# 처음 시작할 때는 진입차수가 0인 노드만 큐에 삽입
for i in range(1, n + 1):
if indegree[i] == 0:
q.append(i)
# 처음 시작할 때 진입차수가 0인 노드는 선수과목이 없는 과목노드임. -> 1학기에 이수 가능.
enrollment_semester[i] = 1
# 큐가 빌 때까지 반복
while q:
now = q.popleft()
result.append(now)
# 해당 노드와 연결 된 노드들의 진입차수를 -1 해주기
for node in graph[now]:
indegree[node] = indegree[node] - 1
if indegree[node] == 0:
q.append(node)
# now 노드와 연결된 노드의 진입차수를 -1을 한 것이 0이 라면, 연결된 노드의 이수가능 학기는 now 노드의 이수가능 학기 + 1을 한 값이다.
enrollment_semester[node] = enrollment_semester[now] + 1
for i in range(1, len(enrollment_semester)):
print(enrollment_semester[i], end = ' ')
topoloy_sort()
※ 전형적인 위상정렬 문제 유형임과 동시에, 위상정렬의 핵심인 진입차수에 대한 내용은 확실히 이해하고 있어야 출력조건에 맞게 출력을 구성할 수 있는 문제.
'Problem Solving' 카테고리의 다른 글
| [백준] 11279번 최대 힙 (feat. 자료 구조, 우선순위 큐) (0) | 2023.03.31 |
|---|---|
| [백준] 1516번 게임 개발 (feat. 위상 정렬, 다이나믹 프로그래밍) (0) | 2023.03.30 |
| [백준] 2623번 음악프로그램(feat. 위상 정렬) (0) | 2023.03.29 |
| [백준] 1766번 문제집(feat. 위상 정렬, heapq) (0) | 2023.03.28 |
| [백준] 2252번 줄 세우기(feat. 위상 정렬) (0) | 2023.03.27 |
댓글
이 글 공유하기
다른 글
-
[백준] 11279번 최대 힙 (feat. 자료 구조, 우선순위 큐)
[백준] 11279번 최대 힙 (feat. 자료 구조, 우선순위 큐)
2023.03.31 -
[백준] 1516번 게임 개발 (feat. 위상 정렬, 다이나믹 프로그래밍)
[백준] 1516번 게임 개발 (feat. 위상 정렬, 다이나믹 프로그래밍)
2023.03.30 -
[백준] 2623번 음악프로그램(feat. 위상 정렬)
[백준] 2623번 음악프로그램(feat. 위상 정렬)
2023.03.29 -
[백준] 1766번 문제집(feat. 위상 정렬, heapq)
[백준] 1766번 문제집(feat. 위상 정렬, heapq)
2023.03.28