[백준] 11660번 구간 합 구하기 5(feat. 누적 합, 다이나믹 프로그래밍)
https://www.acmicpc.net/problem/11660



문제 접근
- 첫 번째 단계
문제의 조건을 정리하면 아래와 같다.
N*N개의 수가 N*N 크기의 표에 채워져 있고,
(x1, y1) 부터 (x2, y2) 까지 합을 구하는 프로그램을 작성해야 한다. (x, y)는 x행 y열을 의미한다.
그리고 입력 조건을 보면, 합을 구해야 하는 연산의 횟수가 M의 범위가 (1<= M <= 100,000)인 것으로 미루어 보았을 때,
1. 구간 합을 구해야 하는데,
2. 구간 합을 구해야 하는 연산의 최대 횟수가 10만번 이므로
누적합, DP를 떠올릴 수 있다.
1. 큰 문제를 작은 문제로 나눌 수 있다.(최적 부분 구조)
문제에서 주어진 조건이다. (x1 ≤ x2, y1 ≤ y2) 이것을 고려하여 생각하자.
(x1, y1), (x2, y2)를
(x1, y1)은 사각형의 좌상단 모서리,
(x2, y2)는 우하단 모서리라고 생각하면,
하나의 합 연산에서 우리가 구해야 하는 계산범위를 유추할 수 있는데
예를 들어, 주어진 (x1, y1), (x2, y2)가 (2, 2), (4, 3) 이라고 가정해보자
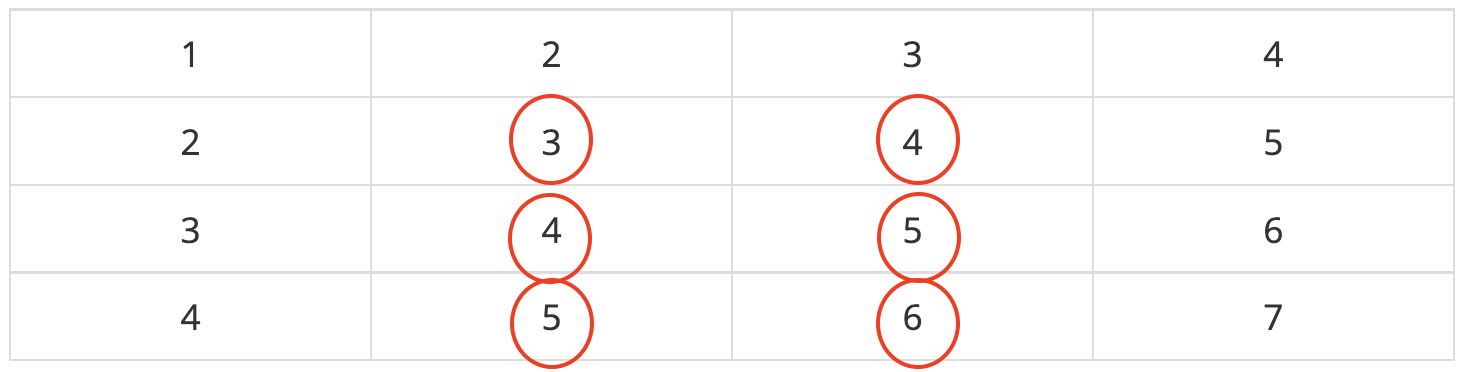
그러면 우리는 빨간색 부분의 합을 구해야 한다.
이때, 하나의 행씩 잘라서 계산 한 후, 합하는 방법을 사용할 수 있을 것이다.
그렇다면 하나의 행을 어떻게 구할지를 생각해보면 되겠다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.(중복되는 부분 문제)
(2, 2), (4, 3)의 합을 구하는 문제에는, (2, 2), (3, 3)을 구하는 문제가 포함되어 있다.
따라서 이 문제는 다이나믹 프로그래밍으로 풀이를 진행할 수 있다.
실제 코드를 작성하기 전, IDE에서 comment로 작성한 부분을 공유하려고 한다.
아래 작성한 conmment를 살펴보자.
3. 점화식을 작성해보자.
'''
1, 2, 3, 4
2, 3, 4, 5
3, 4, 5, 6
4, 5, 6, 7
표가 위와 같다면,
2차원 dp table 을 만들고, 누적합을 계산해서 저장해 놓는다.
dp_table =
[[0, 0, 0, 0, 0]
[0, 1, 3, 6, 10],
[0, 2, 5, 9, 14],
[0, 3, 7, 12, 18],
[0, 4, 9, 15, 22]]
그러면 만약에 (x1, y1), (x3, y2) 가 (2, 2), (4, 3)이면 3 + 4 + 4 + 5 + 5 + 6 = 27
dp_table[x1][y2] - dp_table[x1][y1-1] -> 7
+
dp_table[x2][y2] - dp_table[x2][y1-1] -> 9
+
dp_table[x3][y2] - dp_table[x3][y1-1] -> 11
7 + 9 + 11 = 27
규칙을 찾은 듯 하다.
result = 0
for i in range(x1, x3 + 1):
num = dp_table[i][y2] - dp_talbe[i][y1-1]
result = result + num
'''이렇게 점화식을 먼저 구성한 뒤, 코드를 작성했다.
dp table을 생성한 뒤, 하나의 행에 대하여 누적합을 계산해서 저장해놓고,
이를 실제 연산에 활용하는 방식을 선택했다.
코드를 작성할 때 주의할 점은,
입력받은 실제 테이블과, DP 누적합 테이블을 선언하고 초기화 할 때 인덱스 값을 잘 맞춰줘야 한다.
for문을 돌리기 편하도록 0을 insert 해주는 방식 등, 자기가 편한 방법을 사용하여 초기화 하면 될 것이다.
코드 작성
import sys
# 표의 크기 n, 합을 구해야 하는 횟수 M
n, m = map(int, input().split())
# 표를 저장할 리스트 선언
table = [[0] * (n + 1)]
# 표 입력받아서 table에 저장
for i in range(n):
table_row = list(map(int,sys.stdin.readline().rstrip().split()))
table_row.insert(0, 0)
table.append(table_row)
# dp table 선언
dp_table = [[0] * (n + 1) for _ in range(len(table))]
# dp_table에 누적합 계산
for i in range(1, len(table)):
for j in range(1, len(table[1])):
if dp_table[i][j - 1] != 0:
dp_table[i][j] = dp_table[i][j - 1] + table[i][j]
else:
dp_table[i][j] = table[i][j]
# 합 구하기 m번 수행
for i in range(m):
x1, y1, x2, y2 = map(int, sys.stdin.readline().rstrip().split())
result = 0
for i in range(x1, x2 + 1):
num = dp_table[i][y2] - dp_table[i][y1 - 1]
result = result + num
print(result)'Problem Solving' 카테고리의 다른 글
| [백준] 2559번 수열(feat. 누적 합, 투 포인터, 슬라이딩 윈도우) (0) | 2023.01.13 |
|---|---|
| [백준] 11659번 구간 합 구하기 4(feat. 누적 합) (0) | 2023.01.13 |
| [백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한) (2) | 2023.01.03 |
| [백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘) (0) | 2022.09.14 |
| [백준] 14501번 퇴사(feat. 다이나믹 프로그래밍) (0) | 2022.09.06 |
댓글
이 글 공유하기
다른 글
-
[백준] 2559번 수열(feat. 누적 합, 투 포인터, 슬라이딩 윈도우)
[백준] 2559번 수열(feat. 누적 합, 투 포인터, 슬라이딩 윈도우)
2023.01.13 -
[백준] 11659번 구간 합 구하기 4(feat. 누적 합)
[백준] 11659번 구간 합 구하기 4(feat. 누적 합)
2023.01.13 -
[백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한)
[백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한)
2023.01.03 -
[백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘)
[백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘)
2022.09.14