[백준] 14501번 퇴사(feat. 다이나믹 프로그래밍)
https://www.acmicpc.net/problem/14501
14501번: 퇴사
첫째 줄에 백준이가 얻을 수 있는 최대 이익을 출력한다.
www.acmicpc.net

문제 접근
첫번째 단계
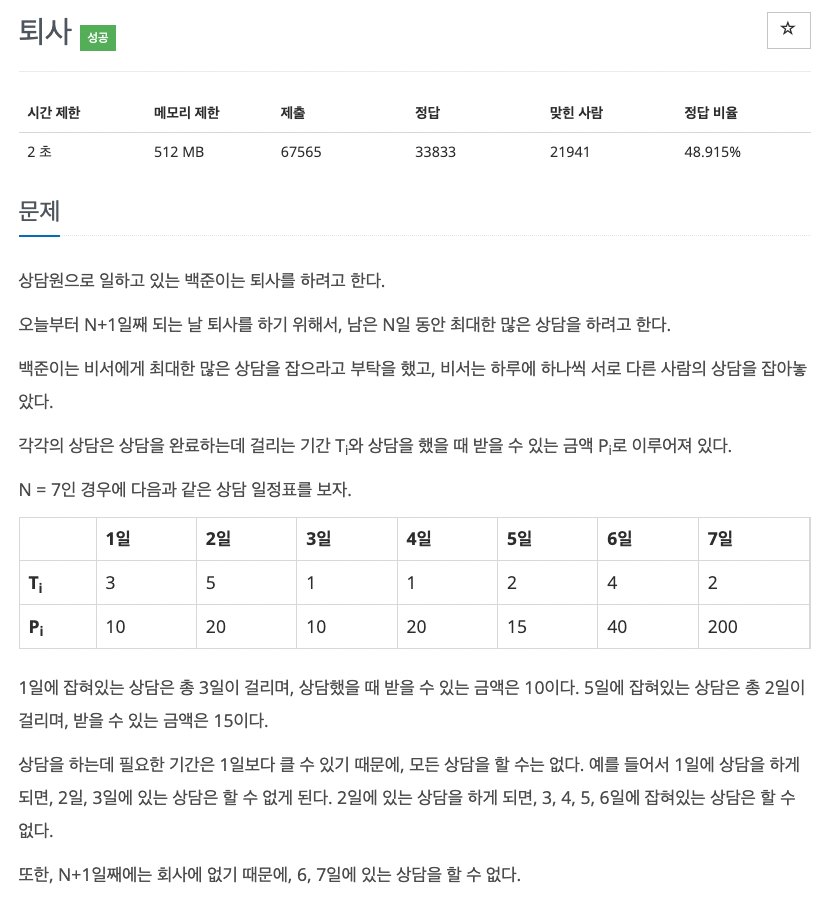
문제를 살펴보자.
특정 날짜의 상담을 진행하면, 해당 날짜의 상담을 진행하는데 소요되는 기간에는 다른 상담은 진행할 수 없다.
그리고 주어진 기간동안 최대한 상담 수익이 많이 나도록 상담을 진행하고, 최대 수익을 도출하는 문제이다.
1. 큰 문제를 작은 문제로 나눌 수 있다.(최적 부분 구조)
이 문제는, 특정 기간의 최대 수익을 도출하는 문제이지만,
특정 상담을 진행 할지, 말지를 구하는 문제로 작게 나눌 수 있다.
따라서, 이 문제는 최적 부분 구조를 만족한다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.(중복되는 부분 문제)
이 문제는, 작은 문제로 나눈 "특정 상담의 진행 여부"가 주어진 기간의 최대 상담 수익을 도출하는데에
중복되어 이용된다.
따라서, 이 문제는 중복되는 부분 문제를 만족한다.
따라서, 이 문제는 다이나믹 프로그래밍으로 풀이를 진행할 수 있다.
두번째 단계
DP Table을 정의 해보자.
즉, 상태를 정의해보자는 의미이다.
i를 근무 가능한 일수라고 생각하면,
dp[i]는 근무 가능한 일수가 i만큼 남았을 때의 최대 비용이 되도록 DP 테이블을 구성하면 될 것이다.
dp[n]은 첫째날부터 마지막날까지 상담을 골라서 했을 때 가지는 최대 수익값 일 것이다.
dp[1]은 근무 가능한 일수가 1일 때 최대 비용을 의미하고, 이때 상담업무는 n일차의 상담업무를 고려하면 된다.
dp[2]는 근무 가능한 일수가 2일 때 최대 비용을 의미하고, 이때 상담 업무는 n-1일차의 상담업무를 고려하면 된다.
그리고 이런식으로 dp[n]을 구하면 마지막 n일차까지 근무했을 때의 최대 비용을 구할 수 있을 것이다.
세번째 단계
점화식을 정의해보자.
이 문제의 상태를 상담 진행의 유무에 따른 최대 수익으로 정의했다.
그렇다면, 코드의 로직은 크게 2가지로 나눌 수 있을 것이다.
- 근무가능한 일수 i가 해당 날짜의 상담소요시간보다 작아서 상담을 진행할 수 없다면,
- dp[i] = d[i - 1] # 상담을 하지 않으므로, 그 전 일자의 최대 수익과 같음
- 근무가능한 일수 i가 해당 날짜의 상담 소요시간보다 커서 해당 상담을 진행할 수 있다면,
- dp[i] = max(dp[i - 1], 해당 상담으로 버는 수익 + dp[i - 상담 소요 시간])
그런데, 문제가 있다.
현재 입력을 그대로 받으면, 위의 점화식을 이용할 수 없다.
왜냐하면,
점화식에 따르면, dp[i]은 근무가능한 일수가 i만큼 남았을 때의 최대수익을 의미하므로
dp[1]은 근무가능한 일수가 1일 일때의 최대수익, 즉 n일차의 최대수익을 의미하는데,
만약 입력을 그대로 받으면, dp[1]은 1일차의 최대수익이 되어, 근무가능한 일수가 n일만큼 남았을 때의 최대 수익으로 정의되기 때문이다.
따라서, 문제의 입력을 거꾸로 뒤집어서 받으면 위에서 정의한 점화식을 그대로 이용할 수 있다.
코드 작성
3가지 방법으로 코드를 작성했고, 그중에 가장 맘에드는 코드를 기재합니다.
import sys
# n 입력 받기
n = int(input())
# 스케줄 입력받기
schedule = []
for i in range(n):
t, p = map(int, sys.stdin.readline().rstrip().split())
schedule.append([t, p])
# 스케줄 입력 거꾸로 뒤집기
schedule.reverse()
schedule.insert(0, [])
# print(schedule)
# dp 테이블 초기화
d = [0] * (n + 1) # DP 배열 또한 인덱스를 날짜로 사용하기 위해 길이를 1 증가
for i in range(1, n + 1):
if i < schedule[i][0]:
d[i] = d[i - 1]
else:
d[i] = max(d[i - 1], schedule[i][1] + d[i - schedule[i][0]])
print(d[n])
'Problem Solving' 카테고리의 다른 글
| [백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한) (2) | 2023.01.03 |
|---|---|
| [백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘) (0) | 2022.09.14 |
| [백준] 1300번 K번째 수(feat. 이분 탐색 Lower-Bound) (0) | 2022.05.10 |
| [백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색 (0) | 2022.05.05 |
| [백준] 1654번 랜선 자르기 (feat.Binary Search)이분 탐색 (0) | 2022.05.01 |
댓글
이 글 공유하기
다른 글
-
[백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한)
[백준] 1904번 01타일(feat. 다이나믹 프로그래밍, 메모리 제한)
2023.01.03 -
[백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘)
[백준] 18353번 병사 배치하기(feat. 다이나믹 프로그래밍, LIS알고리즘)
2022.09.14 -
[백준] 1300번 K번째 수(feat. 이분 탐색 Lower-Bound)
[백준] 1300번 K번째 수(feat. 이분 탐색 Lower-Bound)
2022.05.10 -
[백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색
[백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색
2022.05.05