[백준] 1978번 에라토스테네스의 체- 소수 판별 알고리즘 (소수 찾기)
반응형
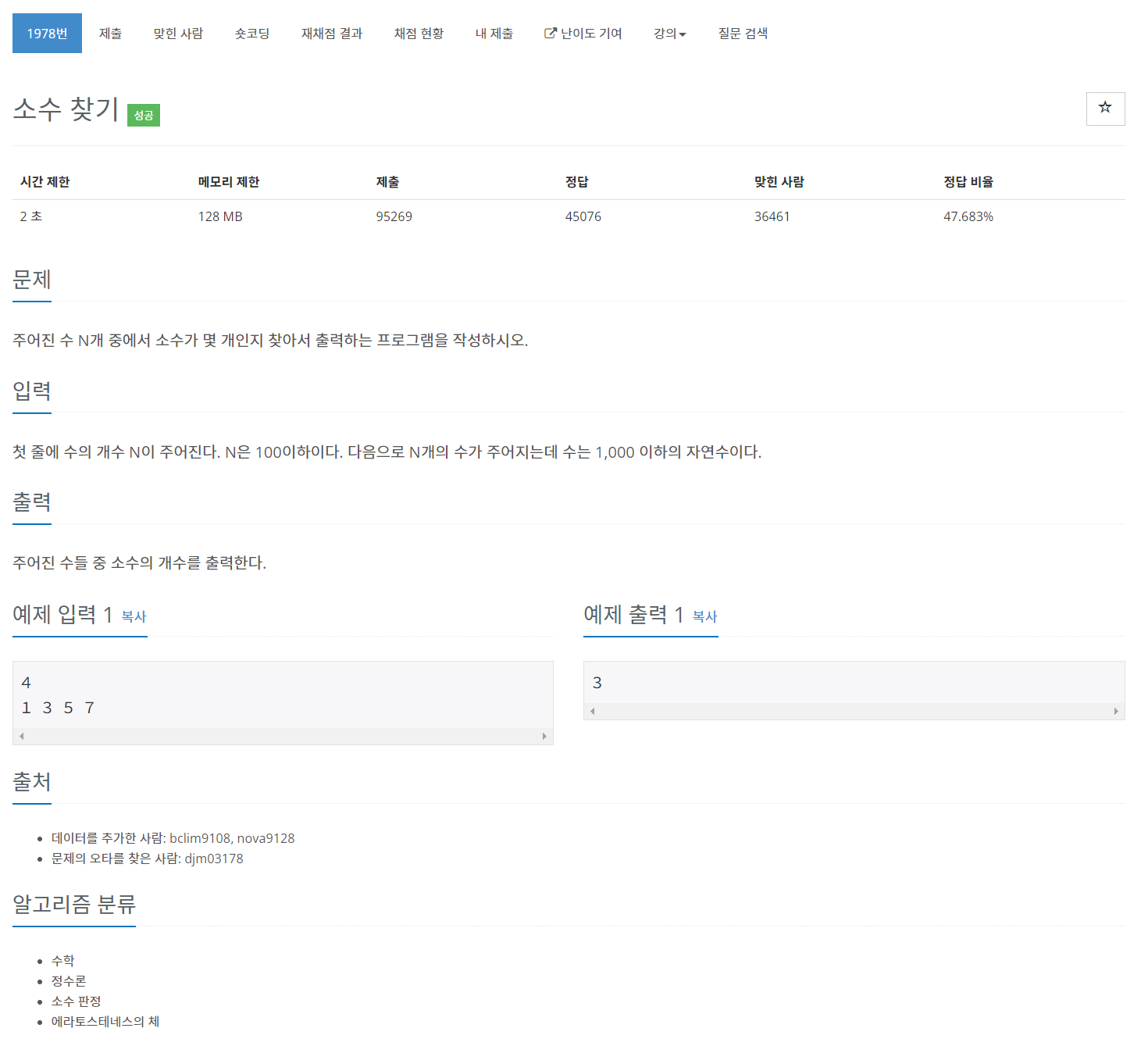
일단 이 문제를 풀 때 처음엔, 에라토스테네스의 체를 이용하지 않고,
일반적인 방법으로 구현해보았다.
case = int(input())
list = list(map(int, (input().split())))
prime_number = []
for i in range(case):
count = 0 # 소수는 1과 자기자신으로만 나뉘는 수이다. 즉 count가 2이면 소수로 판별할 예정
for j in range(1, list[i]+1):
rest = list[i]%j
if rest == 0 :
count = count + 1
else:
pass
if count == 2:
prime_number.append(list[i])
print(len(prime_number))풀이는 완료하고 정답판정을 받았지만,
나는 항상 문제를 풀고나면 내가 작성한 코드가 최선일까? 좀더 효율적인 방법은 없을까? 라는 생각을하며 고민한다.
이 문제는 소수를 판별하는 것이 핵심이다.
소수를 판별하는데에 사용하는 방법론 "에라토스테네스의 체"를 공부하게 되었고,
해당 방법론을 이용하여 추가 코드를 작성하고,
더 나아가, 나의 깃허브의 "Algorithm Interveiw"라는 레포지토리에 "에라토스테네스의 체"를 이용한 소수 판별 함수를 나만의 알고리즘 라이브러리폴더에 추가로 작성했다.
에라토스테네스의 체
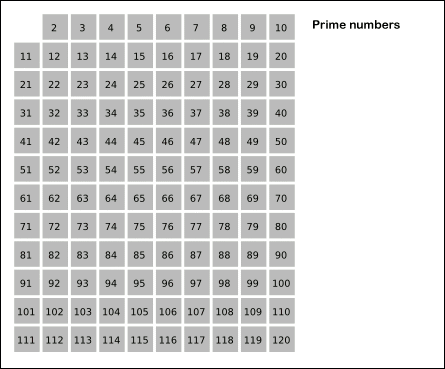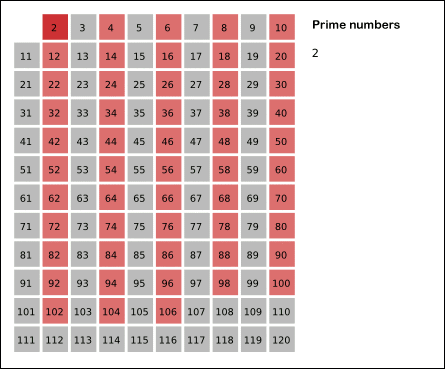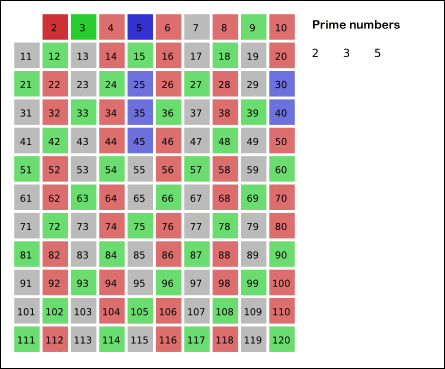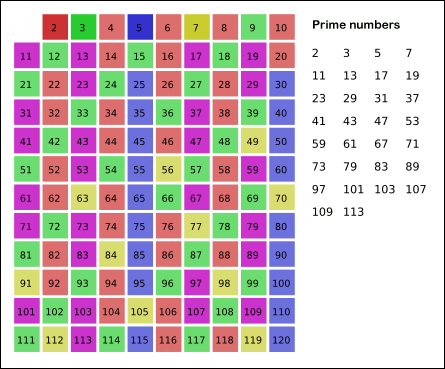
에라토스테네스의 체는 수학에서 소수를 찾는 방법이다. 이때, 소수는 1과 자기자신으로만 나뉘는 자연수를 말한다.
해당 방법론의 알고리즘은 다음과 같다.
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
위 사진의 경우, 11^2 > 120 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.
# 에라토스테네스의 체를 이용한 1978번 풀이
'''
에라토스테네스의 체 알고리즘 동작과정
1. 2부터 N까지의 모든 자연수를 나열한다.
2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
3. 남은 수 중에서 i의 배수를 모두 제거한다.(i는 제거하지 않는다.)
4. 더이상 반복할 수 없을 떄까지 2번과 3번의 과정을 반복한다.
'''
# 에라토스테네스의 체 알고리즘(python)을 이용한 소수 판별 함수(소수 갯수 반환)
def find_prime_number2(a):
import math
case = int(input())
num_list = list(map(int, input().split(' ')))
natural_num = list(range(2, a)) # 자연수 범위를 정한다.(소수는 1이상인 정수이기때문에 1은 뺀상태)
count = 0
for i in range(2, math.ceil(math.sqrt(1000))): # p²≥100인 p의 배수(p를 제외한)까지만 지우면 된다.
for j in natural_num:
if j / i == 1: # 자기 자신으로 나뉘는것은 제외
pass
elif j % i == 0: # 그 이외에 나뉘는 수가 존재하면
natural_num.remove(j) # 그 수는 정수 리스트에서 제거
for k in num_list:
if k in natural_num: # num_list에 natural_num이랑 중복되는 수가 있다면 count +1
# print(k)
count += 1
print(count)
find_prime_number2(1000) # 1000까지의 수 중에서 탐색
항상 나의 코드를 의심하자.
성장하는 방법이다.
반응형
'Problem Solving' 카테고리의 다른 글
| [백준] 2447번 별찍기 문제 재귀 함수 이용해서 풀기 (0) | 2022.01.27 |
|---|---|
| [백준] 10872번 재귀 함수 이용해서 풀기 (feat. 재귀 함수란?) (0) | 2022.01.24 |
| [백준] 1002번 터렛 python (두 원의 교점의 개수 구하기) (0) | 2022.01.22 |
| [백준] 3053번 Python (유클리드 기하학과 택시 기하학) (0) | 2022.01.22 |
| [프로그래머스] 완주하지 못한 선수 문제 풀이(해시 Lv.1) - 파이썬 Python (0) | 2022.01.19 |
댓글
이 글 공유하기
다른 글
-
[백준] 10872번 재귀 함수 이용해서 풀기 (feat. 재귀 함수란?)
[백준] 10872번 재귀 함수 이용해서 풀기 (feat. 재귀 함수란?)
2022.01.24 -
[백준] 1002번 터렛 python (두 원의 교점의 개수 구하기)
[백준] 1002번 터렛 python (두 원의 교점의 개수 구하기)
2022.01.22 -
[백준] 3053번 Python (유클리드 기하학과 택시 기하학)
[백준] 3053번 Python (유클리드 기하학과 택시 기하학)
2022.01.22 -
[프로그래머스] 완주하지 못한 선수 문제 풀이(해시 Lv.1) - 파이썬 Python
[프로그래머스] 완주하지 못한 선수 문제 풀이(해시 Lv.1) - 파이썬 Python
2022.01.19