[백준] 25682번 체스판 다시 칠하기 2(feat. 2차원 배열의 누적 합)
https://www.acmicpc.net/problem/25682


문제 접근
- 첫 번째 단계
문제의 조건은 다음과 같다.
M * N 크기의 보드가 있는데, 어떤 정사각형은 검은색으로 칠해져있고, 나머지는 휜색으로 칠해져있음. 이 보드를 잘라서 K * K 크기의 체스판으로 만들려고함. 정상적인 체스판은 검은색과 휜색이 번갈아서 칠해져 있어야 함. 구체적으로, 각 칸이 검은색과 휜색 중 하나로 칠해져 있으면서, 변을 공유하는 두개의 사각형은 다른 색으로 칠해져 있어야 함. 이 정의를 따르면, 체스판을 색칠하는 경우는 두 가지 뿐이다. 1. 맨 왼쪽 위 칸이 휜색인 경우, 2. 맨 왼쪽 위 칸이 검은색인 경우 보드가 체스판 처럼 칠해져 있다는 보장이 없어서, M * N 크기의 보드를 K * K 로 자른 후, 몇개의 정사각형을 다시 칠해서 체스판으로 만들 것임. 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성 할 것. 입력은 첫째 줄에 N(세로)행, M(가로)열, K 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어짐. (B는 검은색, W는 휜색) 1 <= N, M <= 2000 1 <= K <= min(N, M)
- 두 번째 단계
처음에 이 문제를 접하면, 구간 합 이나 누적 합 이론으로 접근하기 어려울 수 있다.
체스판은 총 2가지 종류가 있다.

시작이 'W'인 것과 'B'인 것이 있다.
그리고 체스판을 배열이라고 생각했을 때,(인덱스가 1이라고 가정)
행+열을 합쳐서 홀수 이면 시작칸의 색깔과 다른 색,
행+열을 합친 값이 짝수이면, 시작칸의 색깔과 같은 색 이다.
이 점을 이용해서 입력받은 체스판에 대해서
시작칸이 'B'인 체스판, 시작칸이 'W'인 체스판 두 가지 경우에 대해서 누적 합을 구한다.
(※ 이때 누적 합 배열이 2차원 배열인 것에 주의해야 한다. 2차원 누적합에 대해서는 맨 아래에 추가 메모 예정)
누적합을 구한 2차원 배열에서 k*k 구간 합 중 가장 작은 값을 구하고,
가장 작은 값을 출력하면 된다.
직접 고민한 과정을 코멘트로 작성해두었다.
''' M * N 크기의 보드가 있는데, 어떤 정사각형은 검은색으로 칠해져있고, 나머지는 휜색으로 칠해져있음. 이 보드를 잘라서 K * K 크기의 체스판으로 만들려고함. 정상적인 체스판은 검은색과 휜색이 번갈아서 칠해져 있어야 함. 구체적으로, 각 칸이 검은색과 휜색 중 하나로 칠해져 있으면서, 변을 공유하는 두개의 사각형은 다른 색으로 칠해져 있어야 함. 이 정의를 따르면, 체스판을 색칠하는 경우는 두 가지 뿐이다. 1. 맨 왼쪽 위 칸이 휜색인 경우, 2. 맨 왼쪽 위 칸이 검은색인 경우 보드가 체스판 처럼 칠해져 있다는 보장이 없어서, M * N 크기의 보드를 K * K 로 자른 후, 몇개의 정사각형을 다시 칠해서 체스판으로 만들 것임. 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성 할 것. 입력은 첫째 줄에 N(세로)행, M(가로)열, K 둘째 줄부터 N개의 줄에는 보드의 각 행의 상태가 주어짐. (B는 검은색, W는 휜색) 1 <= N, M <= 2000 1 <= K <= min(N, M) i) 간단한 예제를 먼저 시뮬레이션 해보자. 4 4 3 BBBB BBBB BBBW BBWB 이면, 3 * 3 크기로 자른 후, 가장 적은 칸을 칠해서 체스판을 만들 수 있는 것의 칸 개수를 구해야 한다. 그러면, 일단은 4 * 4 보드를 3 * 3으로 자를 수 있는 경우를 구하고, 각 경우에 대해서 좌측 상단이 B일 때와, W일 때로 나누어 몇개를 다시 색칠해야 하는지 구해서 비교해볼 수 있을 것이다. 그런데, 문득 들은 생각인데, 처음부터 3 * 3 으로 자를 수 있는 경우를 구하기 전에 입력받은 보드를 아예 좌측 상단이 B인 것과, 좌측 상단이 W인 것으로 나누어 테이블을 만들고, 좌측 상단이 B 인것 BWBW WBWB BWBW WBWB 좌측 상단이 W 인것 WBWB BWBW WBWB BWBW 이렇게 있으면, 누적합 테이블을 b누적합테이블, w누적합 테이블 이렇게 두개 만들어서 정상적인 체스판과 다른 부분의 개수를 카운트해서 갱신하고, 거기서 3 * 3 크기에 해당하는 부분의 누적합을 구해서 가장 작은 부분을 반환하면 되지 않을까? 코드로 구현해보자. 일단 시간초과 난다. ii) 처음 생각한 기본 로직은 맞는 것 같음. 그러면 이제 시간복잡도, 공간복잡도 등을 줄일 수 있는 방법을 생각해보자. 일단, 생각을 해보니까, 체스판의 좌측 상단이 B인 경우와 W인 경우를 나눠서 둘다 구할 필요가 없는 것 같다. 왜냐하면, 체스판의 전체 수 - 좌측 상단이 B로 시작한 체스판에서 수정해야 하는 개수 = w로 직한판 바둑판에서 B로 수정해야 하는 개수 가 성립한다. 그리고, 정상배열도 안만들어 놓아도 될 것 같다. 왜냐하면, 규칙으로 대체 가능하기 때문이다. 결국 로직은, 맨 위, 왼쪽에 흰색일 경우와 검은색일 경우를 배열은 선언하고 비교해서 다른면 1 같은면 0으로 표시를 한다. (인덱스 1부터 시작한다하면, 행과 열 더해서 짝수이면 같고 홀수이면 다르다.) 탐색이 끝나면 그 배열의 누적합을 구한다. 누적합을 구한 2차원 배열에서 K × K 구간합중 가장 작은 값을 구하고 맨위 왼쪽 흰색인 경우와 검은색인 경우중 작은 작은 값을 출력하면된다. --- 2차원 dp 배열을 만들어서 시작점이 W 일때와 B 일때 누적합을 구해준다. 이후 K×K 크기만큼 배열을 탐색해서 누적합의 최소값을 찾는다. dp 배열의 2차원 누적합은 dp[i+1][j+1]=dp[i][j+1]+dp[i+1][j]−dp[i][j]+value 으로 계산해준다. 이때 value 는 체스판이 color 와 같으면 1 아니면 0 을 가지게 된다. value=L[i][j]!=color -> if L[i][j]!=color : value=1 과 같다 K×K 체스판에서의 누적합을 구하는 점화식은 dp[i+K−1][j+K−1]−dp[i+K−1][j−1]−dp[i−1][j+K−1]+dp[i−1][j−1] 와 같다. 기존의 누적합 식에 K를 넣어주었다. 출력은 print(min(Chess('W'),Chess('B'))) 를 통해 최소값을 구할수 있다. 총 2번의 탐색을 하기때문에 시간초과가 발생할수 있으므로 pypy3 로 제출해야한다. '''
코드 작성
import sys sys.maxsize # n, m, k 입력받기 n, m, k = map(int, sys.stdin.readline().rstrip().split()) # 보드 입력받아서 저장하기 board = [] for i in range(n): str = list(sys.stdin.readline().rstrip()) board.append(str) # print(board) def chess(color): prefix_sum = [[0] * (m + 1) for _ in range(n + 1)] for i in range(n): for j in range(m): if (i + j) % 2 == 0: # 인덱스가 0부터 시작하는 것을 고려했을 때, board의 행과 열을 더해서 짝수이면 color와 다르고 (1) value = board[i][j] != color else: # 인덱스가 0부터 시작하는 것을 고려했을 때, board의 행과 열을 더해서 홀수이면 color와 같다 (0) value = board[i][j] == color prefix_sum[i + 1][j + 1] = prefix_sum[i][j + 1] + prefix_sum[i + 1][j] - prefix_sum[i][j] + value # 2차원 배열의 누적합을 구하는 것이다. -prefix_sum[i][j]는 중복으로 더한 부분을 한번 뺴준 것. count = sys.maxsize for i in range(1, n - k + 2): for j in range(1, m - k + 2): count = min(count, prefix_sum[i + k - 1][j + k - 1] - prefix_sum[i + k - 1][j - 1] - prefix_sum[i - 1][j + k - 1] + prefix_sum[i - 1][j - 1]) # 2차원 배열의 누적합 점화식에 k 고려해서 작성한 것임다. return count print(min(chess('B'), chess('W')))
사실 이 문제를 해결하는데에 조금 오래 걸렸다. 1차원 배열 형태의 누적 합 리스트로 변형해서 해결하려고 하다보니,
시간초과 문제 등을 겪었고, 고민 끝에 불필요한 로직을 제거하는 등의 과정을 거쳐서 결국,
이 문제의 핵심은 2차원 배열의 누적 합 이론을 이해하는 것 이라는 것을 깨달았다.
이번에 풀 때는 시간이 좀 걸렸지만, 다음에 어떠한 누적 합 알고리즘 문제를 마주해도, 해결할 자신이 생겼다.
누적 합
arr = [3, 5, 7, 1, 4] sum_list = [3, 8, 15, 16, 20]
위 배열에서 연속된 구간의 합, 예를들어 arr[1]부터 arr[3]까지의 합을 구하려고 한다면 3개의 원소값을 참조해야한다.
이러한 점을 보완하기 위해서 누적합 수열 sum_list를 도입한다.
sum_list[i]는 arr[0]부터 arr[i]까지의 모든 원소의 합을 값으로 갖는다.
또한 arr[i]부터 arr[j]까지의 부분합은 sum_list[j] - sum_list[i-1]로 정의할 수 있다.
누적합을 이용한 빠른 부분합 계산
1차원 배열일 경우 반복문을 통한 구간합이 O(n)이고, 2차원 배열은 O(n^2)이다. 하지만 누적합 배열의 4번째 특징을 사용해서 연속된 임의의 구간의 합을 O(1)의 시간복잡도로 구할 수 있다.
2차원 누적합
위의 개념을 2차원으로 확장해보자.
2차원 배열에 대한 누적 합 배열은 역시 2차원 배열이 된다.
직사각형 형태의 배열에 포함되는 직사각형 구간의 원소의 합을 빠르게 구할 수 있다.
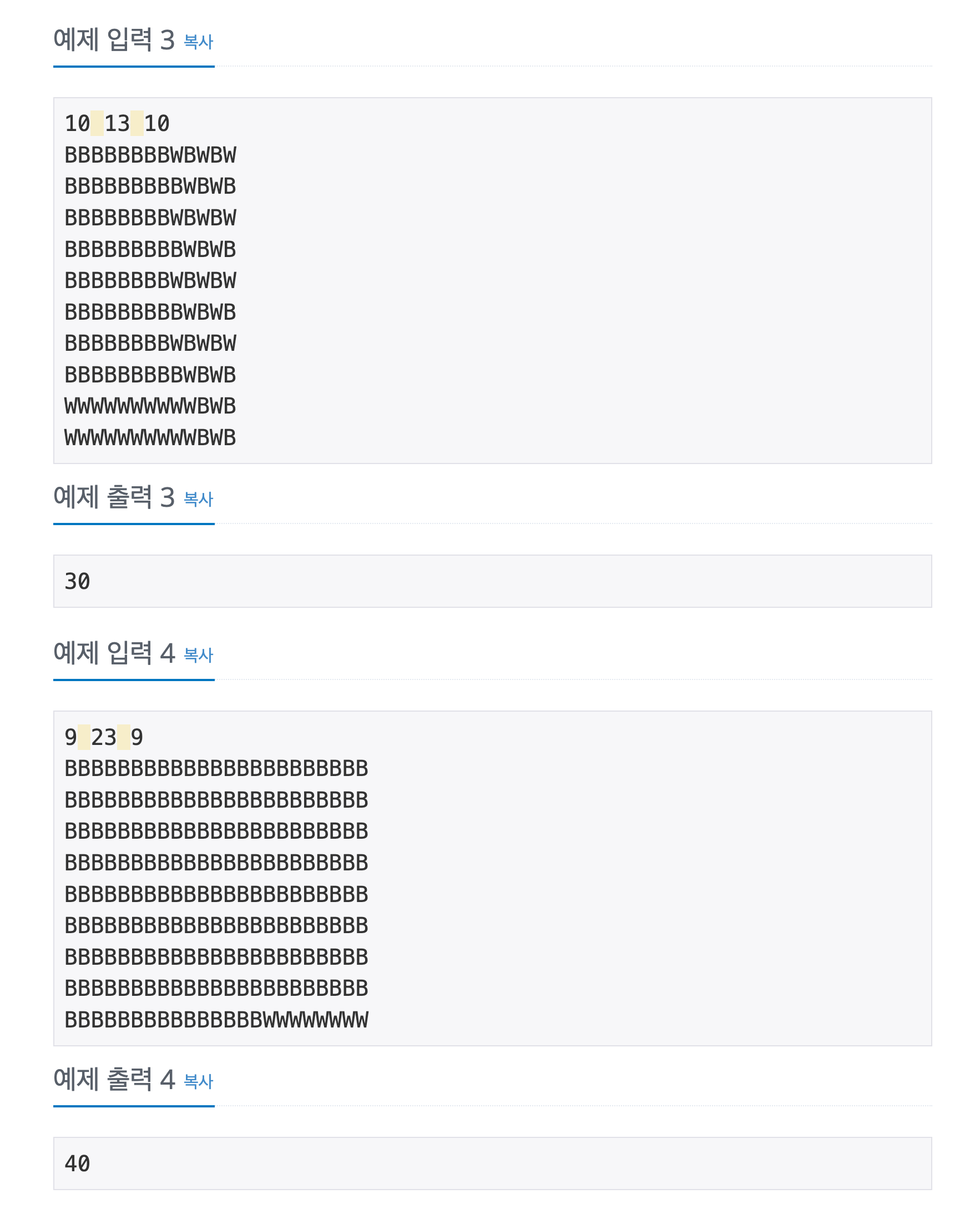
2차원 배열 a(i, j)와 누적합 배열 S(i, j)가 있다고 가정하자.
좌측 상단을 a(1, 1)이라 할 때,
S(i, j)는 a(1, 1)과 a(i, j)를 양 대각 끝 꼭짓접으로 하는 직사각형 범위 면적 안의 모든 a원소의 합으로 정의된다.
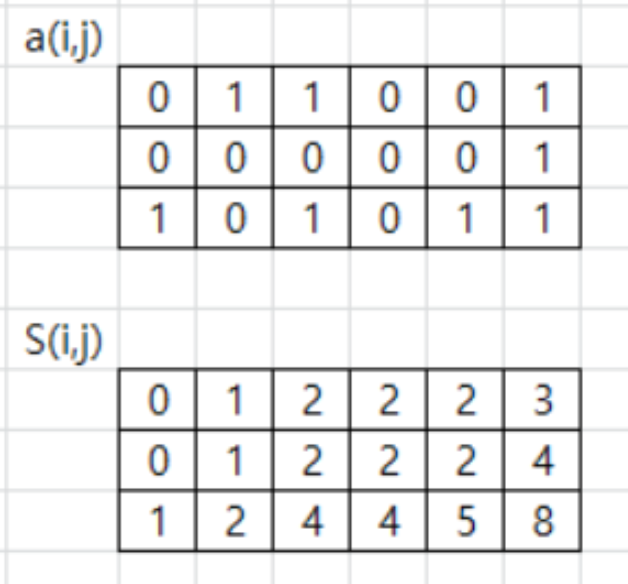
따라서 a(2, 2) ~ a(3, 3)의 부분합을 구해보자.
S(3, 3) 값에서 S(1, 3) 값을 빼고, S(3, 1)값을 뺀다. 이때 S(1, 1)은 S(1, 3)과 S(3, 1)에 의해서 2번 빼지게 된다.
그래서 S(1, 1)을 한번 더해주면, 초록색 부분의 구간합이 된다.
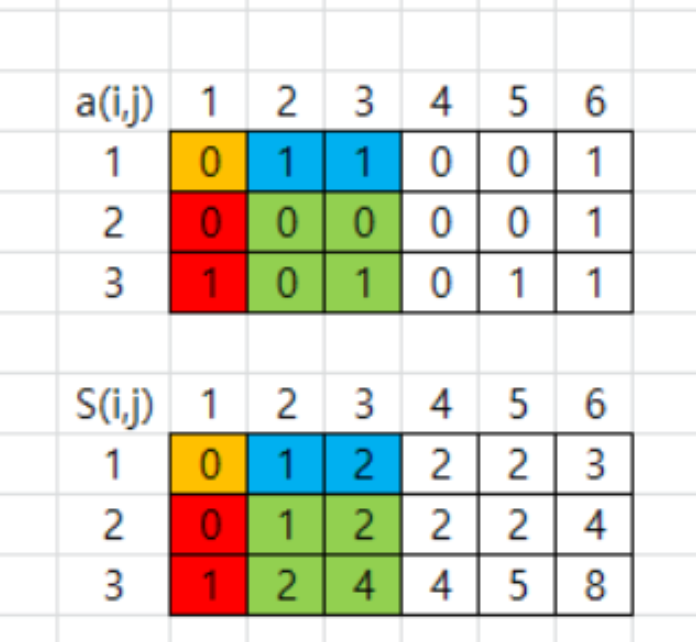
이를 정리하면 다음과 같다.
2차원 배열 arr이 있을 때, arr[x1][y1] 부터 arr[x2][y2]까지의 부분 배열의 합을 Range(x1, y1, x2, y2)라 하자.
그리고 누적합 배열 S로 다음과 같이 정의된다.
Range(x1, y1, x2, y2) = S(x2, y2) - S(x1, y2) - S(x2, y1) + S(x1, y1)
이차원 누적합 배열 구하기
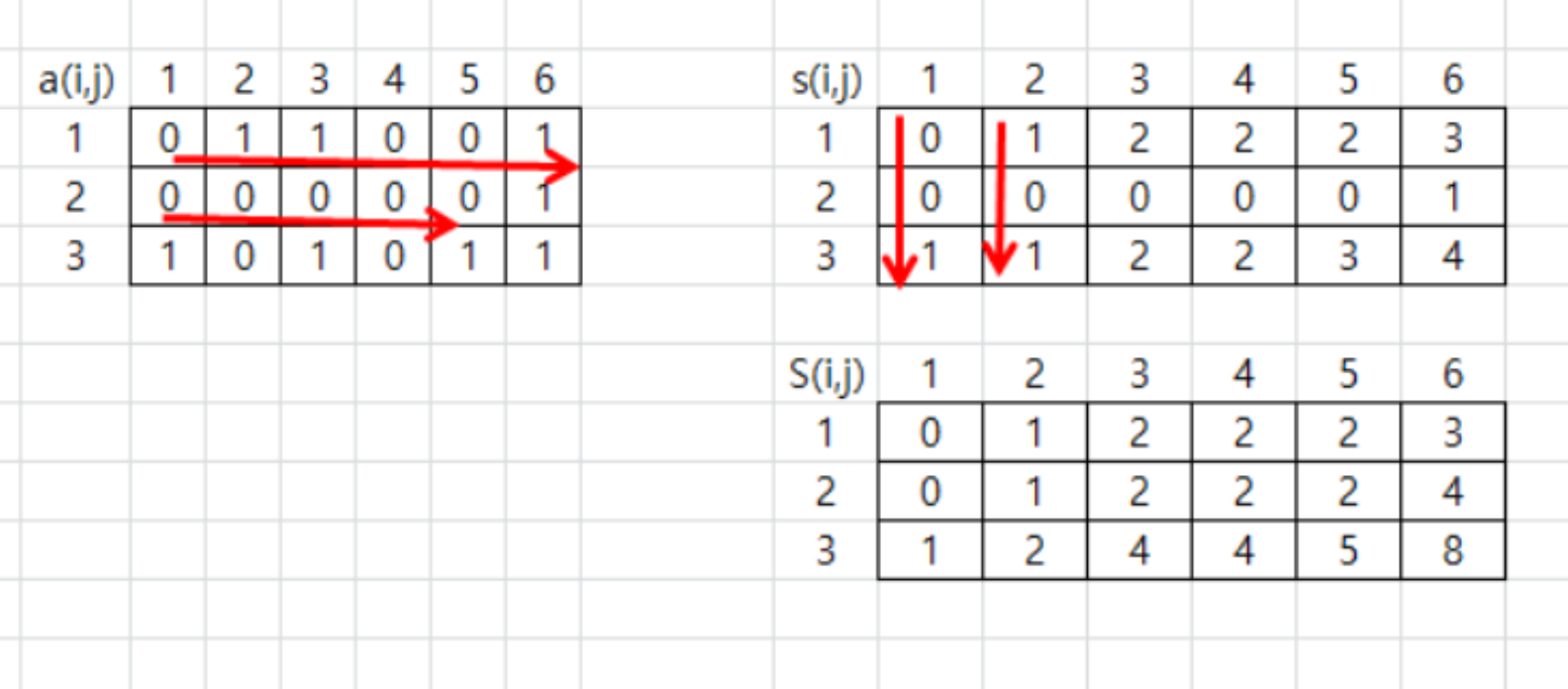
2차원 배열의 누적합 배열을 구하는 방법은 위와 같다.
- a(i, j)에서 행방향으로 누적합을 구한다.
- 행 누적합에 대해서 열방향으로 누적합을 구한다.
arr = [[0, 1, 1, 0, 0, 1], [0, 0, 0, 0, 0, 1], [1, 0, 1, 0, 1, 1]] # 누적합 배열 def get_sum_list(arr: List[List]): # 먼저 행의 합을 구한다. sum_list = [[sum(arr[i][:j + 1]) for j in range(len(arr[0]))] for i in range(len(arr))] # 열의 합을 구한다. for i in range(len(sum_list) - 1): for j in range(len(sum_list[0])): sum_list[i + 1][j] += sum_list[i][j] return sum_list sum_list = get_sum_list(arr) print(sum_list) # 부분합 함수 def accum(S: List[List], x1: int, y1: int, x2: int, y2: int) -> int: # sum_list를 S라 할 때, 꼭짓점 list(x1, y1) ~ list(x2, y2)의 구역합 구하기 # S(x2, y2) - {S(x1, y2) + S(x2, y1)} + S(x1, y1) return S[x2][y2] - (S[x1][y2] + S[x2][y1]) + S[x1][y1] print(accum(sum_list, 0, 1, 2, 4))
복잡도 분석
누적 합은 두 단계로 나누어진다.
- 1. 전처리 : 누적합 배열 S를 구한다.
- 1차원 누적합은 O(n), 2차원 누적합은 O(n^2)의 시/공간 복잡도를 갖는다.
- 2. 계산 : 원하는 구간의 구간합을 계산한다.
- 차원 관계없이 O(1)의 상수 시간 복잡도를 갖는다.
누적 합의 한계
누적 합의 경우 합을 구하는 도중에 원본 배열이 변하는 경우 누적 합을 다시 계산해야 한다. 이 경우에는 세그먼트 트리를 사용해야 한다.
누적 합 정리 출처
'Problem Solving' 카테고리의 다른 글
| [백준] 9370번 미확인 도착지(feat. 다익스트라) (1) | 2023.01.21 |
|---|---|
| [백준] 13549번 숨바꼭질 3(feat. 다익스트라, BFS) (0) | 2023.01.19 |
| [백준] 16139번 인간-컴퓨터 상호작용(feat. 누적 합) (0) | 2023.01.13 |
| [백준] 10986번 수열(feat. 누적 합, 수학) (2) | 2023.01.13 |
| [백준] 2559번 수열(feat. 누적 합, 투 포인터, 슬라이딩 윈도우) (0) | 2023.01.13 |
댓글
이 글 공유하기
다른 글
-
[백준] 9370번 미확인 도착지(feat. 다익스트라)
[백준] 9370번 미확인 도착지(feat. 다익스트라)
2023.01.21 -
[백준] 13549번 숨바꼭질 3(feat. 다익스트라, BFS)
[백준] 13549번 숨바꼭질 3(feat. 다익스트라, BFS)
2023.01.19 -
[백준] 16139번 인간-컴퓨터 상호작용(feat. 누적 합)
[백준] 16139번 인간-컴퓨터 상호작용(feat. 누적 합)
2023.01.13 -
[백준] 10986번 수열(feat. 누적 합, 수학)
[백준] 10986번 수열(feat. 누적 합, 수학)
2023.01.13
댓글을 사용할 수 없습니다.