[백준] 10816번 upperbound - lowerbound (feat.Binary Search)이분 탐색
array1에 있는 데이터중, array2에 있는 데이터와 일치하는 데이터가 있는지 판단하고, array2에 있는 데이터가 각 데이터별로 몇개가 array1에 존재하는지 구하는 문제 유형이었다.
우선, 데이터 탐색 범위가 거의 20000000개 이기 때문에, Binary Search를 이용해야 한다고 판단했다.
그래서 처음 시도한 방법은,
기본적인 Binary Search로 데이터 탐색 후에,
이진탐색 하며 나온 데이터 중, 미리 지정해둔 데이터가 몇 개 나왔는지 count()를 사용해서 tmp리스트에 인덱스 순서대로 기록하는 방식으로 풀이를 시도했는데, 구하고자하는 결과는 잘 도출이 되었지만, 시간초과문제가 발생했다.
이진 탐색과정에서는 문제가 없었는데, 데이터를 기록하려고 작성한 for문에 들어간 count()메서드에서 시간초과가 발생한 것으로 판단했다. count()메서드의 시간복잡도가 O(N)이기 때문으로 판단된다.
그래서 조금더 고민한 결과, upperbound와 lowerbound를 이용하는 방법으로 시도하기로 했다.
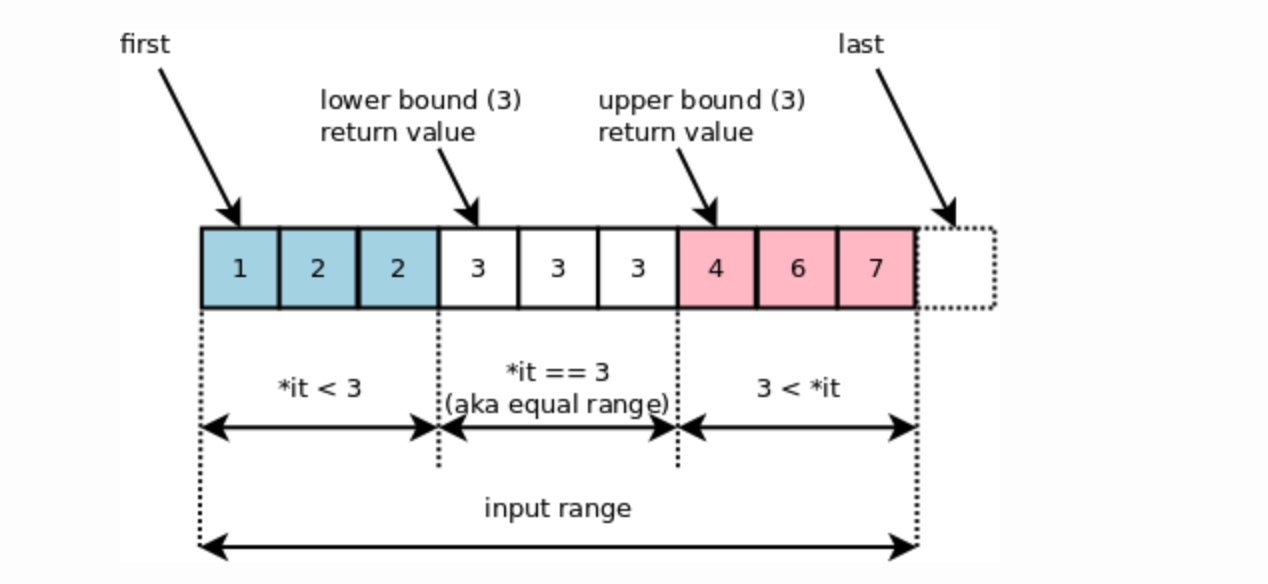
upper_bound탐색과 lower_bound탐색을 이용해서 해당 데이터가 몇 개 존재하는지 판단하는 방법인데, upper_bound는 target값보다 큰 범위를 탐색해서 반환하는 함수이고, lower_bound는 target값보다 같거나 큰 범위를 탐색해서 반환하는 함수이다.
upper_bound - lower_bound 를 하게되면 동일한 데이터가 존재할 시에, 해당 데이터가 몇개 존재하는지를 구할 수있다.
왜냐하면, 데이터가 정렬되어 있다고 가정할시, upper_bound의 반환 값은 갯수를 구하고자 하는 데이터보다 큰 값이 나오는 처음 위치 인덱스를 반환하고, lower_bound의 반환값은 찾고자하는 값과 같거나 큰수가 있는 첫번째 인덱스를 반환하기 때문에
upper_bound - lower_bound를 하게되면 target 데이터의 개수를 구할 수 있다.
이러한 방식으로 문제풀이를 진행했다.
이걸 적용하면, 내가 찾는 숫자의 처음위치-1에서 마지막위치를 각각 시간 복잡도 O(logN)만에 찾아서 뺄셈 계산하면 된다.
upperbound와 lowerbound개념을 잘 이해 해놓아야겠다. (target < lower_bound) (target < upper_bound)
이 개념을 다른 문제들에서 응용 및 변환해서 적용하면 해결될 문제들이 분명 있을테니.
※ Python의 Bisect 모듈을 이용하면 더 간편하긴 한데, 직접 함수를 작성하고 원리를 이해하길 추천함.
# upperbound(큰) - lower_bound(같거나 큰)
# 가지고 있는 카드에 적혀있는 정수
n = int(input())
n_list = list(map(int, input().split()))
n_list_alpha = sorted(n_list)
# 가지고 있는 카드에 적혀있는 정수가 몇개인지 구해야할 정수 리스트
m = int(input())
m_list = list(map(int, input().split()))
# --------------이진 탐색 후 count함수 사용하는 방식인데, 시간초과 발생하는 방식임-------------
# result_list = [0] * m
# def binary_search(array, target, start, end):
# while start <= end:
# mid = (start + end) // 2
# # 찾은 경우 중간점 인덱스 반환
# if array[mid] == target:
# return mid
# # 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
# elif array[mid] > target:
# end = mid - 1
# else:
# start = mid + 1
# return None
# for i in m_list:
# # 해당 번호가 존재 하는지 확인 후, m_list원소값 순서대로 해당 원소값에 해당하는 원소가 n_list에 있을 때마다 result_list의 해당인덱스의 값을 +1
# result = binary_search(n_list_alpha, i, 0, n - 1)
# if result != None:
# result_list[m_list.index(i)] = n_list_alpha.count(i)
#
# print(n_list_alpha)
#----------------------------------------------------------------------------------
def upper_bound(array, target):
start, end = 0, len(array)
while start < end: #start와 end가 만나는 지점이 target값 보다 큰 값이 처음 나오는 위치
# mid = start + (end - start) // 2
mid = (start + end) // 2
if array[mid] <= target:
start = mid + 1
else:
end = mid
return start
def lower_bound(array, target):
start, end = 0, len(array)
while start < end: # start와 end가 만나는 지점이 target값 이상이 처음 나오는 위치
# mid = start + (end - start) // 2
mid = (start + end) // 2
if array[mid] < target:
start = mid + 1
else:
end = mid
return start
# print(n_list_alpha)
# print(upper_bound(n_list_alpha, 3))
# print(lower_bound(n_list_alpha, 3))
for i in m_list:
print(upper_bound(n_list_alpha, i) - lower_bound(n_list_alpha, i), end = ' ')
https://en.wikipedia.org/wiki/Upper_and_lower_bounds
Upper and lower bounds - Wikipedia
Majorant and minorant in mathematics This article is about precise bounds. For asymptotic bounds, see Big O notation. A set with upper bounds and its least upper bound In mathematics, particularly in order theory, an upper bound or majorant[1] of a subset
en.wikipedia.org
'Problem Solving' 카테고리의 다른 글
| [백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색 (0) | 2022.05.05 |
|---|---|
| [백준] 1654번 랜선 자르기 (feat.Binary Search)이분 탐색 (0) | 2022.05.01 |
| '하노이의 탑' 이해하기 (feat. 재귀 함수) (1) | 2022.01.27 |
| [백준] 2447번 별찍기 문제 재귀 함수 이용해서 풀기 (0) | 2022.01.27 |
| [백준] 10872번 재귀 함수 이용해서 풀기 (feat. 재귀 함수란?) (0) | 2022.01.24 |
댓글
이 글 공유하기
다른 글
-
[백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색
[백준] 2110번 공유기 설치 (feat.Binary Search)이분 탐색
2022.05.05 -
[백준] 1654번 랜선 자르기 (feat.Binary Search)이분 탐색
[백준] 1654번 랜선 자르기 (feat.Binary Search)이분 탐색
2022.05.01 -
'하노이의 탑' 이해하기 (feat. 재귀 함수)
'하노이의 탑' 이해하기 (feat. 재귀 함수)
2022.01.27 -
[백준] 2447번 별찍기 문제 재귀 함수 이용해서 풀기
[백준] 2447번 별찍기 문제 재귀 함수 이용해서 풀기
2022.01.27